LEDA - A Library of Efficient Data Types and Algorithms
LEDA ("Library of Efficient Data types and Algorithms") has been developing
since 1988 under the efforts of a group at the Max Planck Institut in
Saarbrucken Germany (including Kurt Melhorn, Stefan Naher, Stefan Schirra,
Christian Uhrig, and Christoph Burnikel). The success of LEDA has been a
direct result of a continuous resource investment on the part of its
algorithmically sophisticated development team. Implemented in C++ using templates, LEDA may be compiled on a wide range of
systems (older compilers may not support templates, but most new C++
compilers provide facilities to implement this feature). The standard
distribution contains source code, installation information, and a complete
user's manual. Please note that LEDA is not in the public domain,
but may be used freely for research and teaching. Commercial licenses are
availabe through the LEDA home page.
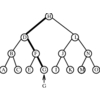
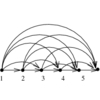
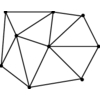
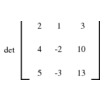
LEDA comprises an extensive collection of data structures and types.
Libraries of algorithms using these data types are provided, with examples
illustrating the ease with which algorithmic tasks may be accomplished given
the LEDA data types.
Download Files (local site)Algorithmic Solutions(now sole distributor of LEDA)Offical Website
Recommended Books
Problem Links
This page last modified on 2008-07-10
.
www.algorist.com
Leda : A Platform for Combinatorial and Geometric Computing
