Matrix Computations by Gene H. Golub and Charles F. Van Loan
Matrix Computations by Gene H. Golub and Charles F. Van Loan
|
 Numerical Recipes in Fortran 90 by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
Numerical Recipes in Fortran 90 by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
|
 Numerical Recipes in Fortran 77 by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
Numerical Recipes in Fortran 77 by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
|
 Numerical Recipes in Pascal by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
Numerical Recipes in Pascal by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
|
 Numerical Recipes in C by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
Numerical Recipes in C by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
|
 Data Structures and Algorithms by A. Aho and J. Hopcroft and J. Ullman
Data Structures and Algorithms by A. Aho and J. Hopcroft and J. Ullman
|
 Permanents by H. Minc
Permanents by H. Minc
|
 Combinatorial Algorithms for Computers and Calculators by A. Nijenhuis and H. Wilf
Combinatorial Algorithms for Computers and Calculators by A. Nijenhuis and H. Wilf
|
 A survey of modern algebra by G. Birkhoff and S. MacLane
A survey of modern algebra by G. Birkhoff and S. MacLane
|
|


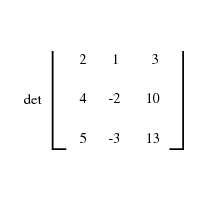

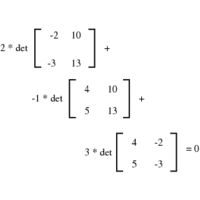
 Matrix Computations
Matrix Computations Numerical Recipes in Fortran 90
Numerical Recipes in Fortran 90 Numerical Recipes in Fortran 77
Numerical Recipes in Fortran 77 Numerical Recipes in Pascal
Numerical Recipes in Pascal Numerical Recipes in C
Numerical Recipes in C Data Structures and Algorithms
Data Structures and Algorithms Permanents
Permanents Combinatorial Algorithms for Computers and Calculators
Combinatorial Algorithms for Computers and Calculators A survey of modern algebra
A survey of modern algebra