1.6.3 Triangulation
INPUT OUTPUT
Input Description:
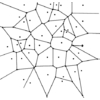
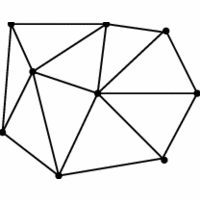
A set of points, or a polyhedron
Problem:
Partition the interior of the point set or polyhedron
into triangles.
Excerpt from
The Algorithm Design Manual:
Triangulation is a fundamental problem in computational
geometry, because the first step in working with complicated
geometric objects is to break them into simple geometric objects.
The simplest geometric objects are triangles in two dimensions,
and tetrahedra in three.
Classical applications of triangulation include finite element
analysis and computer graphics.
A particularly interesting application of triangulation
is surface or function interpolation.
Suppose that we have sampled the height of a mountain at a
certain number of points.
How can we estimate the height at any point $q$ in the plane?
If we project the points on the plane, and then triangulate them,
the triangulation completely partitions the plane into regions.
We can estimate the height of $q$ by interpolating among the
three points of the triangle that contains it.
Further, this triangulation and the associated height values define
a surface of the mountain suitable for graphics rendering.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Computational Geometry : Algorithms and Applications
Computational Geometry in C
Computational Geometry
