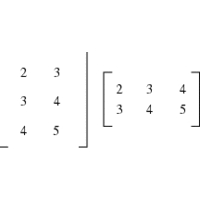
1.2.3 Matrix Multiplication
INPUT OUTPUT
Input Description:
An x x y matrix A, and an y x z matrix B.
Problem:
The x x z matrix A x B.
Excerpt from
The Algorithm Design Manual:
Although matrix multiplication is an important problem in linear algebra, its main significance for combinatorial
algorithms is its equivalence to a variety of other problems, such as transitive closure and reduction, solving
linear systems, and matrix inversion. Thus a faster algorithm for matrix multiplication implies faster algorithms
for all of these problems. Matrix multiplication arises in its own right in computing the results of such
coordinate transformations as scaling, rotation, and translation for robotics and computer graphics.
Asymptotically faster algorithms for matrix multiplication exist, based on clever divide-and-conquer recurrences.
However, these prove difficult to program and require very large matrices to beat the trivial algorithm.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Matrix Computations
Introduction to Algorithms
Arithmetic Complexity of Computations
