1.4.9 Network Flow
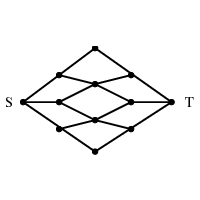
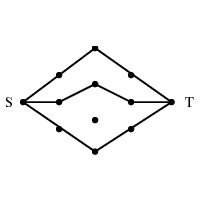
INPUT OUTPUT
Input Description:
A graph G, where each edge (i,j) has a capacity c_{i,j}.
A source node s and sink node t.
Problem:
What is the maximum flow you can route from s to t while
respecting the capacity of each edge.
Excerpt from
The Algorithm Design Manual:
Applications of network flow go far beyond plumbing. Finding the most cost-effective way to ship goods between a
set of factories and a set of stores defines a network flow problem, as do resource-allocation problems in
communications networks and a variety of scheduling problems.
The real power of network flow is that a surprising variety of linear
programming problems that arise in practice can be modeled as network
flow problems, and that special-purpose network flow algorithms can solve
such problems much faster than general-purpose linear programming methods.
Several of the graph problems we have discussed in this book can
be modeled as network flow, including bipartite matching,
shortest path, and edge/vertex connectivity.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Network Coding Theory
Network Flows : Theory, Algorithms, and Applications
Introduction to Algorithms
Flows in Networks
