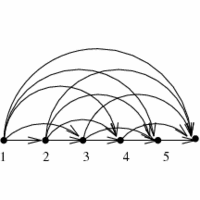
1.4.5 Transitive Closure and Reduction
INPUT OUTPUT
Input Description:
A directed graph G=(V,E).
Problem:
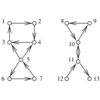
For transitive closure, construct a graph G'=(V,E')
with edge (i,j) \in E' iff there is a directed path from i to j in G.
For transitive reduction, construct a small graph G'=(V,E')
with a directed path from i to j in G' iff (i,j) \in E.
Excerpt from
The Algorithm Design Manual:
Transitive closure can be thought of as establishing a data structure
that makes it possible to solve reachability questions (can I get to x
from y?) efficiently.
After the preprocessing of constructing the transitive closure,
all reachability queries can be answered
in constant time by simply reporting a matrix entry.
Transitive closure is fundamental in propagating the consequences of
modified attributes of a graph G.
For example, consider the graph underlying any spreadsheet model, where the
vertices are cells and there is an edge from cell $i$ to cell j if
the result of cell j depends on cell i.
When the value of a given cell is modified, the values
of all reachable cells must also be updated.
The identity of these cells is revealed by the transitive closure of G.
Many database problems reduce to computing transitive closures,
for analogous reasons.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
Handbook of Theoretical Computer Science : Algorithms and Complexity
The Design and Analysis of Computer Algorithms
