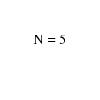Combinatorica
Combinatorica
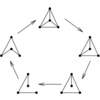
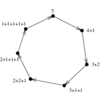
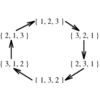
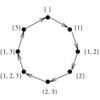
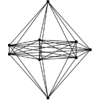
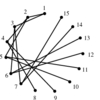
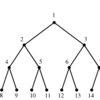
is a collection of over 450 algorithms for discrete mathematics
and graph theory written in Mathematica.
These routines have been designed to work together, enabling one
to experiment with discrete structures and build prototype applications.
Combinatorica has been widely used for both research and education.
Although (in my totally unbiased opinion) Combinatorica is more comprehensive
and better integrated than other libraries of combinatorial algorithms, it
is not the fastest such system available.
Credit for all of these properties is largely due to Mathematica, which
provides a very high-level, functional, interpreted, and thus inefficient
programming language.
Combinatorica is best for finding quick solutions to small problems,
and (if you can read Mathematica code) as a terse exposition of algorithms
for translation into other languages.
The latest version of Combinatorica was codeveloped by Sriram Pemmaraju
and Steven Skiena, and is best described in our book
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica, Cambridge University Press, 2003.
Combinatorica is included with the standard Mathematica distribution in
the directory Packages/DiscreteMath/Combinatorica.m .
The latest version can also be obtained the official website
www.combinatorica.com,
along with many Combinatorica-related resources.
Download Files (local site)Combinatorica distribution
Recommended Books
Problem Links
This page last modified on 2008-07-10
.
www.algorist.com


 Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica