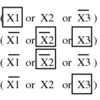
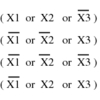1.5.4 Traveling Salesman Problem


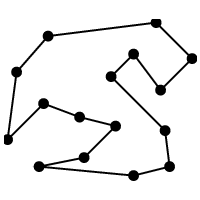
INPUT OUTPUT
Input Description:
A weighted graph G.
Problem:
Find the cycle of minimum cost visiting all of the vertices
of G exactly once.
Excerpt from
The Algorithm Design Manual:
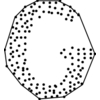
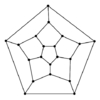
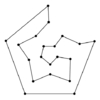
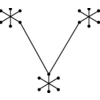
The traveling salesman problem is the most notorious NP-complete problem.
This is a function of its general usefulness, and because
it is easy to explain to the public at large.
Imagine a traveling salesman who has to visit each of a given set of cities
by car.
Although the problem arises in transportation applications, its most
important applications arise in optimizing the tool paths
for manufacturing equipment.
For example, consider a robot arm assigned to solder all the connections on
a printed circuit board.
The shortest tour that visits
each solder point exactly once defines the most efficient path for the robot.
A similar application arises in minimizing the amount of time taken by
a graphics plotter to draw
a given figure.
Recommended Books
Related Links
Georgia Tech's Traveling Salesman Problem page
Lodi and Punnan's TSP Software
Library for testing TSPs
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com





 The Traveling Salesman Problem and Its Variations
The Traveling Salesman Problem and Its Variations The Traveling Salesman Problem : A Guided Tour of Combinatorial Optimization
The Traveling Salesman Problem : A Guided Tour of Combinatorial Optimization