About the Book

The Stony Brook Algorithm Repository

Steven Skiena
Stony Brook University
Dept. of Computer Science

1.4.2 Topological Sorting

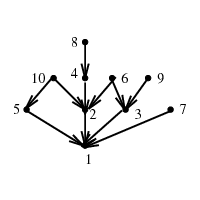
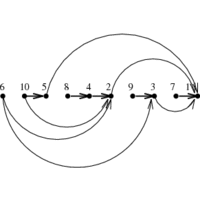
INPUT                    OUTPUT

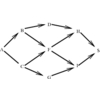
Input Description: A directed, acyclic graph G=(V,E) (also known as a partial order or poset).

Problem: Find a linear ordering of the vertices of V such that for each edge (i,j) \in E, vertex i is to the left of vertex j.

Excerpt from The Algorithm Design Manual: Topological sorting arises as a natural subproblem in most algorithms on directed acyclic graphs. Topological sorting orders the vertices and edges of a DAG in a simple and consistent way and hence plays the same role for DAGs that depth-first search does for general graphs.

Topological sorting can be used to schedule tasks under precedence constraints. Suppose we have a set of tasks to do, but certain tasks have to be performed before other tasks. These precedence constraints form a directed acyclic graph, and any topological sort (also known as a linear extension) defines an order to do these tasks such that each is performed only after all of its constraints are satisfied.