1.2.2 Bandwidth Reduction

INPUT OUTPUT
Input Description:
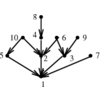
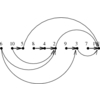
A graph G=(V,E), representing an n x n matrix M of
zero and non-zero elements.
Problem:
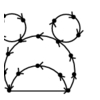
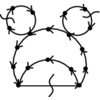
Which permutation p of the vertices of V minimizes
\max_{(i,j) \in E} |p(i) - p(j)|, or equivalently the length of the
longest edge when the vertices are ordered on a line.
Excerpt from
The Algorithm Design Manual:
Bandwidth reduction lurks as a hidden but important problem for both graphs and matrices, and it is important to
see how it arises so as to properly recognize it. Applied to matrices, it permutes the rows and columns of a sparse
matrix so as to minimize the distance b of any nonzero entry from the center diagonal. This is important
in
solving linear systems, because Gaussian elimination can be performed in O(n b2) on matrices of
bandwidth b. This is a big win over the general O(n3) algorithm if b << n.
Bandwidth minimization on graphs arises in more subtle ways. Arranging a set of n circuit components in
a line
on a circuit board so as to minimize the length of the longest wire (and hence time delay) is a bandwidth
problem, where each vertex of our graph corresponds to a circuit component and there is an edge for every wire
linking two components.
Recommended Books
None Available
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com