1.7.1 Set Cover
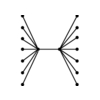
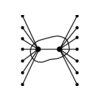
INPUT OUTPUT
Input Description:
A set of subsets S_1, ..., S_m of the universal
set U = \{1,...,n\}.
Problem:
What is the smallest subset of subsets T \subset S such
that \cup_{t_i \in T} t_i = U?
Excerpt from
The Algorithm Design Manual:
Set cover arises when you try to efficiently acquire
or represent items that have been packaged in a fixed set of lots.
You want to obtain all the items, while buying as few lots as possible.
Finding a cover is easy, because you can always buy one of each lot.
However, by
finding a small set cover you can do the same job for less money.
An interesting application of set cover is Boolean logic minimization.
We are given a particular Boolean function of k variables, which
for each of the 2k possible input vectors describes whether the desired
output is 0 or 1.
We seek the simplest circuit that exactly implements this function.
One approach is to find a disjunctive normal form (DNF) formula
on the variables and their complements,
such as x1 \bar x2 + \bar{x}1 \bar{x}2.
We could build one ``and'' term for each input vector and then
``or''
them all together, but
we might save considerably by factoring out common subsets of variables.
Given a set of feasible ``and'' terms, each of which covers a subset of the
vectors we need, we seek to ``or'' together the smallest number of terms
that realize the function.
This is exactly the set cover problem.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Introduction to Algorithms
Discrete Optimization Algorithms with Pascal Programs
Combinatorial Optimization: Algorithms and Complexity
