1.7.2 Set Packing
INPUT OUTPUT
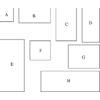
Input Description:
A set of subsets S = S_1, ..., S_m of the universal
set U = \{1,...,n\}.
Problem:
What is the largest number of mutually disjoint subsets
from S?
Excerpt from
The Algorithm Design Manual:
Set packing problems arise in partitioning applications, where we
need to partition elements under strong constraints on what is an
allowable partition.
The key feature of packing problems is that no elements are permitted
to be covered by more than one set.
We seek a large subset of vertices such that each edge is adjacent
to at most one of the selected vertices.
To model this as set packing, let the universal set consist of all
edges of G, and subset Si consist of all edges incident on
vertex vi.
Any set packing corresponds to a set of vertices with no edge in common,
in other words, an independent set.
Scheduling airline flight crews to airplanes is another application of
set packing.
Each airplane in the fleet needs to have
a crew assigned to it, consisting of a
pilot, copilot, and navigator.
There are constraints on the composition of possible crews,
based on their training to
fly different types of aircraft, as well as any personality conflicts.
Given all possible crew and plane combinations, each represented by a
subset of items, we need an assignment such that each plane and each
person is in exactly one chosen combination.
After all, the same person cannot be on two different planes,
and every plane needs a crew.
We need a perfect packing given the subset constraints.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Discrete Optimization Algorithms with Pascal Programs
