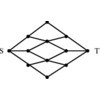
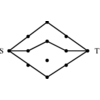
1.4.6 Matching
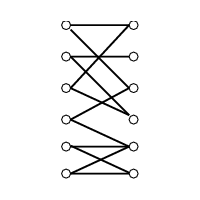
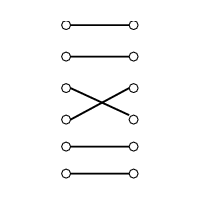
INPUT OUTPUT
Input Description:
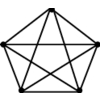
A (weighted) graph G=(V,E).
Problem:
Find the largest size set of edges S \in E such that
each vertex in V is incident to at most one edge of S.
Excerpt from
The Algorithm Design Manual:
Consider a set of employees, each of whom is capable of
doing some subset of the tasks that must be performed.
We seek to find an assignment of
employees to tasks such that each task is assigned to a unique employee.
Each mapping between an employee and a task
they can handle defines an edge,
so what we need is a set of edges with no employee or job
in common, i.e. a matching.
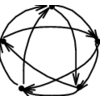
Efficient algorithms for constructing matchings are based on constructing augmenting paths in graphs.
Given a (partial) matching M in a graph G, an augmenting path P
is a path of edges where every odd-numbered edge (including the first and
last edge) is not in M, while every even-numbered edge is.
Further, the first and last vertices must not be already in M.
By deleting the even-numbered edges of P from M and
replacing them with the odd-numbered edges of P, we enlarge the size
of the matching by one edge.
Berge's theorem states
that a matching is maximum if and only if it does not contain any augmenting
path.
Therefore, we can construct maximum-cardinality matchings by
searching for augmenting
paths and stopping when none exist.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Algorithms in Java, Third Edition (Parts 1-4)
Network Flows : Theory, Algorithms, and Applications
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
Introduction to Algorithms
The Stable Marriage Problem: structure and algorithms
Introduction to Algorithms
Matching Theory
Data Structures and Network Algorithms
Combinatorial Optimization: Algorithms and Complexity
