1.5.3 Vertex Cover
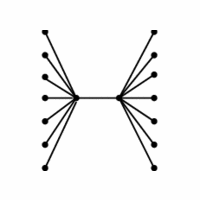
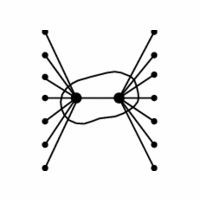
INPUT OUTPUT
Input Description:
A graph G=(V,E).
Problem:
What is the smallest subset S \subset V such that
each e \in E contains at least one vertex of S?
Excerpt from
The Algorithm Design Manual:
Vertex cover is a special case of the more general set cover problem, which takes as input an arbitrary
collection of subsets S = (S_1, \ldots, S_n) of the universal set U = \{1,\ldots,m\}.
We seek the smallest subset of subsets from $S$ whose union is U. Set cover arises in many applications,
including Boolean logic minimization.
To turn vertex cover into a set cover problem, let U be the complete set of edges, and create $S_i$ to be
the set of edges incident on vertex i. A set of vertices defines a vertex cover in graph $G$ iff the
correspondinag subsets define a set cover in the given instance. However, since each edge can be in only two
different subsets, vertex cover instances are simpler than general set cover. The primary reason for
distinguishing between the two problems is that vertex cover is a relative lightweight among NP-complete problems,
and so can be effectively solved.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Approximation Algorithms
Approximation Algorithms for NP-hard Problems
Combinatorial Optimization: Algorithms and Complexity
