The Scheduling of Machine Execution in Prolog

Recall that above we described a conceptual model of how Prolog executes nondeterministic programs by talking of a growing and shrinking set of deterministic procedural machines. In order to completely understand how Prolog executes these nondeterministic programs, we must look more carefully at how this growing and shrinking set of machines is actually executed. Clearly Prolog is not executed by actually have a set of hardware machines that grows and shrinks. (While it would be nice, the physics of such machines has not yet been worked out.) Instead these multiple machines must somehow be simulated, or emulated, by a single hardware machine having just one processor.

The Prolog engine keeps track of the states of these multiple machines and uses them to simulate the machine executions. Let's first consider the way Prolog keeps track of the state of a single machine. We can model execution of a single machine by ``expanding'' procedures. When a procedure is called, the actual parameters are matched with the formal parameters. All variables that get values in the matching process, occurrences in the body of the procedure being called and variables in the calling procedure, are replaced by those values. And the procedure call is replaced by the body of the procedure. The explanation is complex but the idea is simple: procedure calls are replaced by procedure bodies, with the variables appropriately set. For example.....

Now that we have seen how a single machine executes, the real question is in what order does it emulate the multiple machines. Clearly when a query first starts, there is just one machine to execute it. What happens when that machine encounters a procedure defined by multiple clauses? At that point there are several machines to be executed. In what order does Prolog execute them? I.e., how are they scheduled?

===================

The formal counterpart of Prolog execution is the SLD search tree. Each node in the search tree corresponds to a state of one of the machines. Each path through the search tree corresponds to the execution sequence of one of the machines. A branching node in the tree corresponds to a choice point, when a machine is duplicated to create instances of itself that will explore the various alternatives.

Let's look at a simple example to see how this works for the append program when it is called with a final list and it is asked to find all pairs of lists that concatenate to form the given list.

Consider the query:

     | ?- append(X,Y,[a,b]).

First we have to determine a way to represent the states of the individual procedural machines. The state of execution of a procedural program is normally kept by a current instruction pointer and a stack of activation records associated with active procedures, which indicate values of local variables and also where to return when the procedure exits. For our Prolog programs we will use a very abstract representation that will enable us to understand the machine's operations without getting lost in encoding details. We will keep an instance of the variables of the original query and the sequence of procedure calls that remain to be done to complete the machine's computation. So the state of the initial machine is:

     answer(X,Y) :- append(X,Y,[a,b]).

We use the :- to separate the query variables, which are grouped by answer, from the sequence of procedure calls that remain to be done. Initially the only thing to be done is the initial procedure call. We move a machine to its next state by taking the first procedure call after the :- in the machine state, matching it against the head of the chosen clause that defines the procedure, and replacing that call by the body of the clause, with the variables appropriately updated. Thus one step of computation replaces a procedure call by the sequence of procedure calls that make of the body of its definition, with the variables appropriately updated according to the parameter passing method.

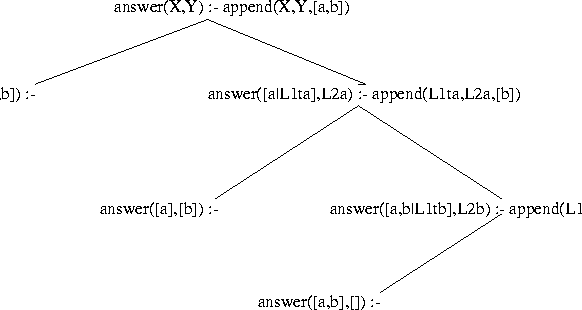
So let's now consider the execution of the above query. The execution will be a tree of machine states, with the above machine state at the root. This tree is shown in Figure 2.1.

  

Figure 2.1: SLD tree for the query: append(X,Y,[a,b]).

Prolog explores this tree in a top-down left-to-right order. The left-to-right order of children of a node corresponds to the order in which clauses for the called procedure appear in the text of the program. This is implemented in the Prolog engine by maintaining a stack of alternatives; whenever new alternative computation states are generated, it pushes them onto the stack, and whenever it needs another alternative, it takes the top one from the stack. So the Prolog engine begins by taking the first (and only) state off the stack and matching the first procedure, append(X,Y,[a,b]), with the heads of the appropriate procedure definitions (i.e., clauses). For each one that matches, it pushes a new state on the stack, replacing the procedure call by the body of the procedure, updating the variables accordingly. Now this first procedure call matches both clauses, so we generate two new states as children of the root state:

answer([],[a,b]) :- .
answer([a|L1ta],L2a) :- append(L1ta,L2a,[b]).

The second state comes from the second clause, and the procedure call is replaced by the single procedure call in the body of the second clause defining append. The first state comes from the first clause, which has no procedure call in its body, so this state has no procedure call to do, and thus is a successful final state of the Prolog program. The arguments of the answer template contain the values of the variables of the original query, and so constitute the final answer of this machine. Here they are [] and [a,b], which do indeed concatenate to generate [a,b], as expected. Prolog will print this answer out, remove this state from the stack and continue expanding the next state on the top of the stack, here the second child of the root node.

Now consider that state:

answer([a|L1ta],L2a) :- append(L1ta,L2a,[b]).

It was generated by matching the original procedure call with the second clause for append. In a procedural language, whenever a procedure is called, the procedure gets a new set of local variables, and in Prolog it is the same. I've indicated that here by giving the variables in the clause new names, by adding `a' to the end of their original names. Each time I take a clause, I'll have to rename the variables to new ones, so we don't have unintended collisions, and I'll do this by adding a new letter suffix.

Again Prolog expands this state by replacing the first procedure call by the bodies of matching clauses. Again both clauses for append match this one so we get two new states on the stack:

answer([a],[b]) :- .
answer([a,b|L1tb],L2b) :- append(L1tb,L2b,[]).

The top one is again an answer, since it has no procedures left to call, and its values for the result variables are: [a] and [b], which again do concatenate to form the desired [a,b].

After the answer is printed and the state removed from the stack, the next state:

answer([a,b|L1tb],L2b) :- append(L1tb,L2b,[]).

is expanded. Now this procedure call matches only the first of the append clauses; the second fails to match because the third argument in the call is [] but in the procedure head is [X|L3t]. So the new stack is just:

answer([a,b],[]) :- .

The top state is an answer, which gets popped and displayed, and then the stack is empty, indicating that Prolog has completely finished traversing the SLD tree and thus with evaluating the query. It has simulated all the deterministic procedural machines to completion.

Stepping back a bit and thinking about the SLD tree, we can quite easily describe the tree by giving an operation that can be applied to a subtree to extend it. Then we can define the SLD tree as the result of applying this operation to an initial (trivial) tree, and all resulting trees until no operation is applicable. This operation is called PROGRAM CLAUSE RESOLUTION.

Definition 2.1.1   (Program Clause Resolution)  Given a tree with a node labeled
$A :- A_1, A_2, \ldots, A_n$, and a rule in the program of the form $H :- B_1, B_2, \ldots, B_k$, and given that H and B₁ match with matching variable assignment $\theta$, then add a new node as a child of this one and label it with $(A :- B_1, B_2, \ldots, B_k, A_2, \ldots, A_n)\theta$, if it does not already have a child so labeled. Note that the matching variable assignment is applied to all the goals in the new label. $\Box$

Notice that the entire tree of Figure 2.1 is developed by applying this rule to the trivial tree consisting of the single node answer(X,Y) :- append(X,Y,[a,b]). So we can think of Prolog as applying this PROGRAM CLAUSE RESOLUTION rule over and over again (in a top-down backtracking manner) to the initial query to trace out the SLD tree.

The example we have used here has a relatively simple execution and Prolog executions can get considerably more complex, but all the basics have been illustrated.