 |
Two FSM's are said to be equivalent if they accept exactly the same set of strings. Given any nondeterministc FSM, it is always possible to find an equivalent one that has no epsilon transitions. In fact, given a machine as defined and represented above, we can easily define such an equivalent epsilon-free machine. So given a machine named mach and defined in m/4, mis/2 and mfs/2, we will define the transitions, initial state and final state for its epsilon-free version named efree(mach) as follows:
% epsilon-free machines
% first define emoves as any sequence of epsilon transitions
emoves(_,State,State).
emoves(Mach,State0,State) :-
emoves(Mach,State0,State1),
m(Mach,State1,'',State).
% define the transition relation of the efree machine
m(efree(Mach),State,Symbol,TargState) :-
emoves(Mach,State,State1),
m(Mach,State1,Symbol,State2),
Symbol \== '',
emoves(Mach,State2,TargState).
% define the initial and final states of the efree machine
mis(efree(Mach),IS) :- mis(Mach,IS).
mfs(efree(Mach),FS) :- mfs(Mach,FS1),emoves(Mach,FS,FS1).
mfs(efree(Mach),FS) :- mfs(Mach,FS1),emoves(Mach,FS1,FS).
The predicate emoves/3 defines for any machine the set of pairs
of states such that the machine can move from the first state to the
second state without consuming any symbols in the input string. Then
with this definition, the rule defining transitions says that an
epsilon-free machine can move from State to TargState on Symbol if it
can move from State to State1 using only epsilon moves, can move from
State1 to State2 on seeing Symbol (which is not epsilon) and can
make epsilon moves from State2 to TargState.
The initial state of the epsilon-free machine is exactly the initial state of the original machine. The final state of the epsilon-free machine is any state from which you can get to a final state of the original machine using only epsilon transitions, or any state you can get to from a final state using only epsilon transitions.
For example:
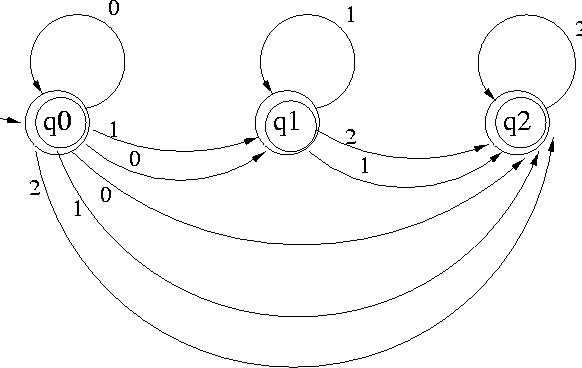
warren% xsb XSB Version 1.6.0 (96/6/15) [sequential, single word, optimal mode] | ?- [automata]. [automata loaded] yes | ?- m(efree(m0s1s2s),So,Sym,Ta),writeln(m(efree(m0s1s2s),So,Sym,Ta)),fail. m(efree(m0s1s2s),q0,0,q0) m(efree(m0s1s2s),q0,0,q1) m(efree(m0s1s2s),q0,0,q2) m(efree(m0s1s2s),q1,1,q1) m(efree(m0s1s2s),q1,1,q2) m(efree(m0s1s2s),q2,2,q2) m(efree(m0s1s2s),q0,1,q2) m(efree(m0s1s2s),q0,1,q1) m(efree(m0s1s2s),q1,2,q2) m(efree(m0s1s2s),q0,2,q2) no | ?- mis(efree(m0s1s2s),IS),writeln(mis(efree(m0s1s2s),IS)),fail. mis(efree(m0s1s2s),q0) no | ?- mfs(efree(m0s1s2s),FS),writeln(mfs(efree(m0s1s2s),FS)),fail. mfs(efree(m0s1s2s),q2) mfs(efree(m0s1s2s),q0) mfs(efree(m0s1s2s),q1) no | ?-
The diagram for efree(m0s1s2s) is shown in Figure
5.2.