 |
We represent a finite state machine using three relations:
By including a MachineName in each tuple, we can use these relations to represent a number of different FSM's. This will be convenient later.
We will use the symbol '' (the atom with the empty name) as a
pseudo-symbol to represent epsilon transitions, transitions a machine
can make without consuming any input symbol.
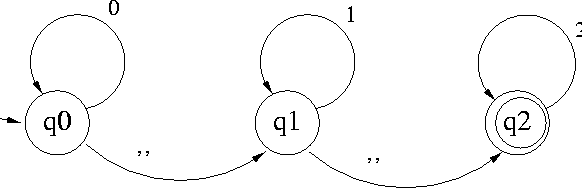
For example, the following relations represent the machine pictured in Figure 5.1, which we will call m0s1s2s, since it recognizes strings made up of a string of 0's followed by a string of 1's followed by a string of 2's:
m(m0s1s2s,q0,0,q0). m(m0s1s2s,q0,'',q1). m(m0s1s2s,q1,1,q1). m(m0s1s2s,q1,'',q2). m(m0s1s2s,q2,2,q2). mis(m0s1s2s,q0). mfs(m0s1s2s,q2).
We represent strings with two relations. Again we will name strings for convenience.
string(s1,0,0,1). string(s1,1,0,2). string(s1,2,1,3). string(s1,3,1,4). string(s1,4,1,5). string(s1,5,2,6).and string ``021'', which we'll name s2, would be represented by:
string(s2,0,0,1). string(s2,1,2,2). string(s2,2,1,3).
stringlen(s1,6). stringlen(s2,3).
A FSM is said to accept a string if it executes in the following way: it starts in the initial state, and makes a transition to the next state along a path labeled by the symbol it is looking at. It consumes that symbol and then makes another transition based on the next symbol in the string. It continues in this way until all symbols are consumed, and if the machine is then in a final state, the string is accepted; otherwise it is rejected. If there is an epsilon-transition from one state to another, the machine can make such a transition without consuming a symbol of the input.
Now we can easily write a specification in XSB that defines when a machine accepts a string, as follows:
:- auto_table.
% A machine accepts a string if the machine starts in the initial state,
% recognizes the string, ending in a final state and has consumed the
% entire string.
accept(MachineName,StringName) :- mis(MachineName,StateStart),
recognize(MachineName,StringName,StateStart,StateFinal,0,StringFinal),
mfs(MachineName,StateFinal),
stringlen(StringName,StringFinal).
% recognize(MachineName,StringName,MState0,MState,SLoc0,SLoc) is true
% if machine MachineName started in state MState0 can transition to
% state MState by recognizing the substring from location SLoc0 to SLoc
% of the string named StringName.
% The empty input string
recognize(_,_,MState,MState,SLoc,SLoc).
% regular transitions
recognize(MachineName,StringName,MState0,MState,SLoc0,SLoc) :-
string(StringName,SLoc0,Symbol,SLoc1),
m(MachineName,MState0,Symbol,MState1),
recognize(MachineName,StringName,MState1,MState,SLoc1,SLoc).
% Epsilon transitions
recognize(MachineName,StringName,MState0,MState,SLoc0,SLoc) :-
m(MachineName,MState0,'',MState1),
recognize(MachineName,StringName,MState1,MState,SLoc0,SLoc).
The definition of accept says that a machine accepts a string
if StateStart is the initial state of the indicated machine, and the
machine transits from StateStart to StateFinal while recognizing the
string starting from 0 and ending at StringFinal, and StateFinal is a
final state of the machine, and StringFinal is the length of the
string.
The definition of recognize/6 describes how a machine moves
through its states while recognizing (or generating) a sequence of
symbols. The first clause says that for any machine and any string,
when the machine stays in the same state, no symbols of the string are
processed. The second clause says that a machine moves from MState0
to MState recognizing a substring if the next symbol in the substring
is Symbol, and there is a transition of the current machine on that
Symbol that takes the machine from MState0 to MState1, and the machine
recognizes the rest of the substring from that state MState1 getting
to MState. The third clause handles epsilon transitions; it says that
a machine moves from MState0 to MState recognizing a substring if
there is an epsilon transition from MState0 to a MState1 and the
machine recognizes the entire string from MState1 to MState.
For example, accept(m0s1s2s,s1) succeeds, but accept(m0s1s2s,s2) fails:
warren% xsb XSB Version 1.6.0 (96/6/15) [sequential, single word, optimal mode] | ?- [automata]. [automata loaded] yes | ?- accept(m0s1s2s,s1). ++Warning: Removing incomplete tables... yes | ?- accept(m0s1s2s,s2). no | ?-
This is a right-recursive definition of recognize/6, so it
might seem that this should not need tabling. And indeed for this
particular machine and string, Prolog would evaluate this definition
just fine. However, there are machines for which tabling is required.
Can you give an example of such a machine?
Also, it is possible to give this specification in a left-recursive manner. That is also an exercise for the reader.