More on Transitive Closure

We saw in the previous section how XSB with tabling will correctly and finitely execute a transitive closure definition even in the presence of cyclic data. Actually, this is only a simple example of the power of tabled evaluation.

We can write another version of transitive closure:

    :- table avoids/2.
    avoids(Source,Target) :- owes(Source,Target).
    avoids(Source,Target) :-
        avoids(Source,Intermediate),
        owes(Intermediate,Target).

This one is left recursive. A Prolog programmer would not consider writing such a definition, since in Prolog it is guaranteed to be nonfinite. But with tabling, this definition works fine. As a matter of fact, it is generally a more efficient way to express transitive closure than is right recursion. In this section we will look at various versions of transitive closure and compare their efficiency.

Let's consider the evaluation of the same avoids query on the same owes data as above, but using the left-recursive definition of avoids.

Figure 3.6 shows the state of the initial server when it first encounters a request to a server.

  

Figure 3.6: Beginning of evaluation of avoids(andy,Ya) for left-recursive transitive closure definition

Note that this time the request to a server is to the server for avoids(andy,Ya), and this is the server itself. (The names of the variables don't matter when finding a server; they are just ``placeholders'', so any server with the same arguments with the same pattern of variables works.) The server does have an answer already computed, so it can send it back to the requester (itself), and that results in the tree of Figure 3.7.

  

Figure 3.7: More of the evaluation of avoids(andy,Ya) for left-recursive transitive closure definition

Now the new leaf, created by the returned answer, can be expanded (by PROGRAM CLAUSE RESOLUTION) yielding a new answer, avoids(andy,carl). This answer can be returned to the (only) requester for this server, and that generates a second child for the requester node; this state is shown in Figure 3.8.

  

Figure 3.8: More of the evaluation of avoids(andy,Ya) for left-recursive transitive closure definition

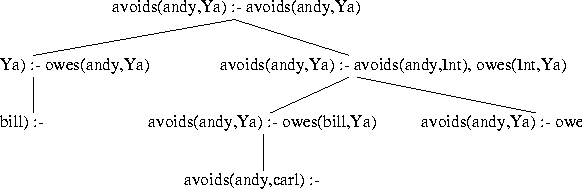Now this node can be expanded (by Program Clause Resolution) to obtain the tree of Figure 3.9

  

Figure 3.9: Final forest for avoids(andy,Ya) for left-recursive transitive closure definition

Here we have generated another answer, but it is the same as one we've already generated, so returning it to the requester node will not generate any new children. All operations have been applied and no more are applicable, so we have reached the final forest of trees, a forest consisting of only one tree. Note that we have the correct two (distinct) answers: that andy avoids bill and andy avoids carl.

The right-recursive definition and the left-recursive definition of avoids both give us the correct answers, but the left-recursive definition (for this query) generates only one tree, whereas the right recursive definition generates several. It seems as though the left-recrsive definition would compute such queries more efficiently, and this is indeed the case.

Consider transitive closure over an owes relation that defines a cycle. E.g.,

owes(1,2).
owes(2,3).
owes(3,4).
...
owes(99,100).
owes(100,1).

defines a graph with a cycle of length 100. How would the trees in the forest look after evaluation of a query to avoids(1,X) using the right-recursive transitive closure definition? For each n between 1 and 100, there is a tree with root: avoids(n,Y). And each such tree will have 100 leaf answer nodes. So the forest will have at least 100² nodes, and for a cycle of length n the forest would be of size O(n²).

What does the forest look like if we use the left-recursive definition? It has one tree with root, avoids(1,Y), and that tree has 100 answer leaves. Generalizing from the tree of Figure 3.9, we see that it is a very flat tree, and so for a cycle of length n, the tree (forest) would be of size O(n). The left-recursive definition is indeed the more efficient to compute with. Indeed the complexity of a single-source query to the left-recursive version of transitive closure is linear in the number of edges in the graph reachable from the source node.