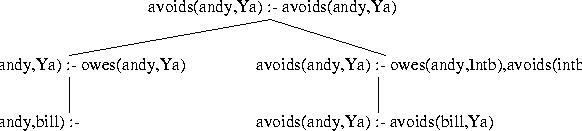XSB tabled execution as the execution of concurrent machines

We understood a Prolog evaluation as a set of executing deterministic procedural machines, increasing in number as one of them executes a multiply-defined procedure, and decreasing in number as one of them encounters failure. Then we saw how it was implemented by means of a depth-first backtracking search through the tree of SLD computations, or procedure evaluations. To add the concept of tabling, we have to extend our computational model. Tabling execution is best understood as computation in a concurrent programming language. Nontabled predicates are evaluated exactly as in SLD, with the intuition of a procedure call. Evaluating a tabled predicate is understood as sending the goal to a cacheing goal server and then waiting for it to send back the answers. If no server for the goal exists, then one is created and begins (concurrently) to compute and save answers. If a server for this goal already exists, none needs to be started. When answers become available, they can be (and eventually will be) sent back to all waiting requesters. So tabled predicates are processed ``asynchronously'', by servers that are created on demand and then stay around forever. On creation, they compute and save their answers (eliminating duplicates), which they then will send to anyone who requests them (including, of course, the initiating requester.)

Now we can see tabled execution as organized around a set of servers. Each server evaluates a nondeterministic procedural program (by a depth-first backtracking search through the alternatives) and interacts with other servers asynchronously by requesting answers and waiting for them to be returned. For each answer returned from a server, computation continues with that alternative.

The abstraction of Prolog computation was the SLD tree, a tree that showed the alternative procedural machines. We can extend that abstraction to tabled Prolog execution by using multiple SLD trees, one for each goal server.

Let's trace the execution of the program for reachability on the simple graph in owes/2, given the query :- avoids(andy,Ya). Again, we start with a query and develop the SLD tree for it until we hit a call to a tabled predicate. This is shown in Figure 3.1.

Then rules are found which match the first goal on the right-hand-side of the rule. In this case there are two, which when used to replace the expanded literal, yield two children nodes:

Computation continues by taking the first one and expanding it. Its selected goal (the first on the right-hand side) matches one rule (in this case a fact) which, after replacing the selected goal with the (empty) rule body, yields:

Then computation continues by using the stack to find that the second child of the root node:

**Figure 3.1:** Tree for avoid(andy,Ya) goal server
$\begin{figure}\centerline{\epsfbox{figures/slgf-owe1.eps}} \end{figure}$

Now the selected goal for this node is avoids(bill,Ya), and avoids is a tabled predicate. Therefore this goal is to be solved by communicating with its server. Since the server for that goal does not exist, the system creates it, and schedules it to compute its answers. This computation is shown in Figure 3.2.

**Figure 3.2:** Tree for avoid(bill,Ya) goal server
$\begin{figure}\centerline{\epsfbox{figures/slgf-owe2.eps}} \end{figure}$

This computation sequence for the goal avoid(bill,Y) is very similar to the previous one for avoid(andy,Y). The first clause for avoids is matched, followed by the one fact for owes that has bill as its first field, which generates the left-most leaf of the tree of the figure. This is an answer which this (concurrently executing) server could immediately send back to the requesting node in Figure 3.1. Alternatively, computation could continue in this server to finish the tree pictured in Figure 3.2, finally generating the right-most leaf:

**Figure 3.3:** Tree for avoids(carl,Ya) goal server
$\begin{figure}\centerline{\epsfbox{figures/slgf-owe3.eps}} \end{figure}$

This computaton is beginning to look familiar; again the form of the computation tree is the same (because only one clause matches owes(carl,Y)). Again an answer, avoids(carl,bill), is produced (and is scheduled to be returned to its requester) and computation continues to the right-most leaf of the tree with the selected goal of avoids(bill,Ya). This is a tabled goal and so will be processed by its server. But now the server does exist; it is the one Figure 3.2. Now we can continue and see what happens when answers are returned from servers to requesters. Note that exactly when these answers are returned is determined by the scheduling strategy of our underlying concurrent language. We have thus far assumed that the scheduler schedules work for new servers before scheduling the returning of answers. Other alternatives are certainly possible.

Now in our computation there are answers computed by servers that need to be sent back to their requesters. The server for avoids(bill,Ya) (in Figure 3.2) has computed an answer avoids(bill,carl), which it sends back to the server for avoids(andy,Ya) (in Figure 3.1). That adds a child to the rightmost leaf of the server's tree, producing the new tree shown in Figure 3.4.

**Figure 3.4:** Updated tree for avoid(andy,Ya) goal server
$\begin{figure}\centerline{\epsfbox{figures/slgf-owe4.eps}} \end{figure}$

Computation continues with answers being returned from servers to requesters until all answers have been sent back. Then there is nothing left to do, and computation terminates. The trees of the three servers in the final state are shown in Figure 3.5.

**Figure 3.5:** Final state for all goal servers for query avoids(andy,Ya)
$\begin{figure}\centerline{\epsfbox{figures/slgf-owe5.eps}} \end{figure}$

Let's be more precise and look at the operations that are used to construct these server trees. We saw that the SLD trees of Prolog execution could be described by giving a single rule, PROGRAM CLAUSE RESOLUTION, and applying it over and over again to an initial node derived from the query. A similar thing can be done to generate sets of server trees that represent the computation of tabled evaluation. For this we need three rules:

Definition 3.0.1 (Program Clause Resolution) Given a tree with a node labeled
$A :- A_1, A_2, \ldots, A_n$ , which is either a root node of a server tree or A₁ is not indicated as tabled. Also given a rule in the program of the form $H :- B_1, B_2, \ldots, B_k$ , (with all new variables) and given that H and B₁ match with matching variable assignment $\theta$ , then add a new node as a child of this one and label it with $(A :- B_1, B_2, \ldots, B_k, A_2, \ldots, A_n)\theta$ , if it does not already have a child so labeled. Note that the matching variable assignment is applied to all the goals in the new label. $\Box$

Definition 3.0.2 (Subgoal Call) Given a nonroot node with label $A :- A_1, A_2, \ldots, A_n$ , where A₁ is indicated as tabled, and there is no tree with root A₁ :- A₁, create a new tree with root A₁ :- A₁. $\Box$

Definition 3.0.3 (Answer Clause Resolution) Given a non-root node with label
$A :- A_1, A_2, \ldots, A_n$ , and an answer of the form B :- in the tree for A₁, then add a new node as child of this node labeled by $(A :- A_2, \ldots, A_n)\theta$ , where $\theta$ is the variable assignments obtained from matching B and A₁ (if there is not already a child with that label.) $\Box$

So for example the trees in Figure 3.5 are constructed by applying these rules to the initial tree (root) for the starting goal. XSB can be understood as efficiently constructing this forest of trees. We have seen that XSB with tabling will terminate on a query and program for which Prolog will loop infinitely. It turns out that this is not just an accident, but happens for many, many programs. For example, here we've written the transitive closure of owes using a right recursive rule, i.e., the recursive call to avoids follows the call to owes in the second rule defining avoids. We could also define avoids with a rule that has a call to avoids before a call to owes. That definition would not terminate in Prolog for any graph, but with tabling, it is easily evaluated correctly.