Hamiltonian Cycle / Gray Code Animation
A Hamiltonian Cycle is a cycle that visits each node exactly once. Here we show a Hamiltonian cycle on a 5-dimensional hypercube. Note that it starts by completely traversing the 4-dimensional hypercube on the left before reversing the traversal on the right subcube.

Hamiltonian cycles on hypercubes provide constructions for Gray codes, namely orderings of all subsets of n items such that neighboring subsets differ in exactly one element.

Hamilitonian cycle is an NP-complete problem, so no worst-case efficient algorithm exists to find such a cycle. In practice, we can find Hamiltonian cycles in modest-sized graphs by using backtracking with clever pruning to reduce the search space.

Download:

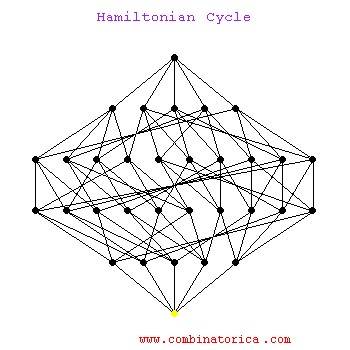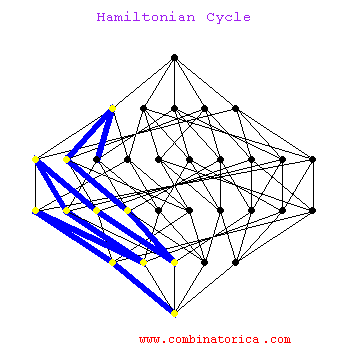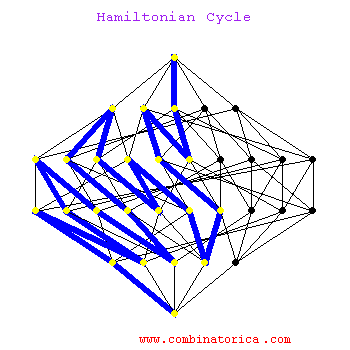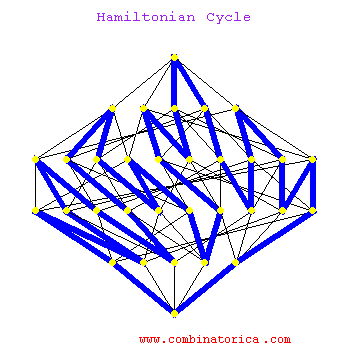
  ham.gif - The Animation.
  ham.nb - Notebook file.

These animations were produced using Combinatorica -- see www.combinatorica.com and our book Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica for more information.

Check out our dfs/bfs, connected components, Hamiltonian cycle, Eulerian cycle, shortest path, transitive closure, and minimum spanning tree animations!