After some general discussions about the organization of the reading group, Steve Skiena began the problem session by asking a few questions about planar graphs. A graph is said to be planar if it can be drawn in the plane without any two edges crossing (or intersecting each other).
QUESTION 1: If the vertices of a planar graph are fixed, how many bends are needed to draw the graph without any intersections?
For instance, 
is a planar graph, but if you require the edges to
be straight, and you fix the vertices to be in the shape of a square
(see Figure 1), then you cannot draw without
intersections. However, if we allow the edges to ``bend'', then it
becomes possible to draw the graph without crossings.
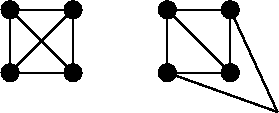
Figure 1: is a planar graph which cannot be drawn (using straight line edges)
without crossings if the vertices are arranged as in the left image.
However, if we allow a bend in one of the edges, as in the right
image, we can draw without intersections.
Joe Mitchell believed that this problem was already discussed in the reading group in previous years, and that it is related to finding minimum-link embeddings. We continued discussing the problem and asked a more basic question.
QUESTION 2: If the vertices of a planar graph are fixed, can we always draw it without intersections (using bends)?
Several people began looking at 
with one edge removed, since
is the smallest non-planar graph. Regardless of whether it was
an interior or exterior edge which was removed, we found
that it was possible to draw the graph without crossings.
Figure 2 shows a drawing of with an exterior edge
removed and the corresponding drawing in which there are no
intersections.
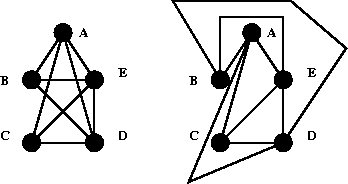
Figure 2: The left image is of with an exterior edge removed. The right
image shows how we can draw the graph without intersections by using
bends.
Joe went to the board and began describing a method by which we could always ``untangle'' a planar graph so that regardless of the vertices' locations, we could always draw the graph without crossings:
Start with a planar graph, and then ``drag'' the vertices of the graph into a line so that they are in order: 1, 2, 3, etc. This operation of ``dragging'' the vertices to their proper position on the line does not change the topology of the graph - the new graph is isomorphic to the original graph.
Eventually, more people began to believe that this approach would work, but argued about whether the answer to the following question was quadratic, cubic, or even polynomial.
QUESTION 3 How many ``bends'' does this approach yield?
Saurabh Sethia suggested taking a graph and ``compressing'' it so that the vertices lie on a line in no particular order. This compressed graph still has O(n) edges, but between vertices i and i+1, there can be O(n) ``thickness''.
Joe then mentioned that for any permutation of points in the plane,
there is a simple chain using at most 
links. Therefore,
if we ``compress'' the graph and then use this result, we end up with
links.