Visual Correlation Analysis on the Correlation Map

Abstract: Correlation analysis can reveal the complex relationships that often exist among the variables in multivariate data. However, as the number of variables grows, it can be difficult to gain a good understanding of the correlation landscape and important intricate relationships might be missed. We previously introduced a technique that arranged the variables into a 2D layout, encoding their pairwise correlations. We then used this layout as a network for the interactive ordering of axes in parallel coordinate displays. Our current work expresses the layout as a correlation map and employs it for visual correlation analysis. In contrast to matrix displays where correlations are indicated at intersections of rows and columns, our map conveys correlations by spatial proximity which is more direct and more focused on the variables in play. We make the following new contributions, some unique to our map: (1) we devise mechanisms that handle both categorical and numerical variables within a unified framework, (2) we achieve scalability for large numbers of variables via a multi-scale semantic zooming approach, (3) we provide interactive techniques for exploring the impact of value bracketing on correlations, and (4) we visualize data relations within the sub-spaces spanned by correlated variables by projecting the data into a corresponding tessellation of the map.

Teaser: The images below show the correlation map and its multi-scale zooming capabilities for a car dataset. The correspomding parallel coordinate displays below provide a view onto the actual data. The number of vertical axes is controlled by the attributes shown in the correlation map.

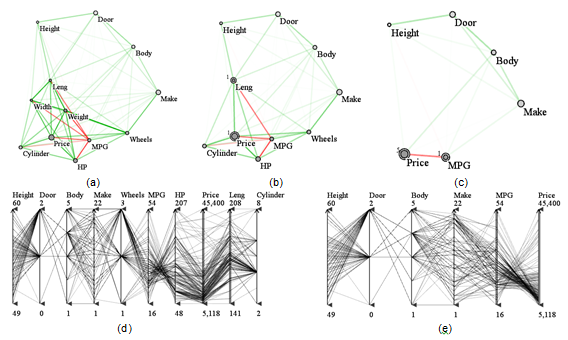
The original correlation map is shown in panel (a). As one zooms out, (a), (b) and (c) show the result sequences of correlation map views. From (c) we can see that variables Weight, Length, Width, Price, Cylinder, and HP have been merged into one (Price) because all are positively correlated. Although MPG is close to them, it has a negative correlation with the others, so it is not merged. But MPG and Drive Wheel have positive correlation, so they also merge into one (MPG). The number of variables packed into the representative variable is given by the small number in the upper left corner of representative vertex. Finally, panels (d) and (e) show the corresponding Parallel Coordinate displays of (b) and (c), respectively, where the display in (e) has fewer axes due to the zooming out.

Video: Watch it to get a quick overview:

Case study: Multivariate Analysis of University Data, see here

Paper: Z. Zhang, K. McDonnell, E. Zadok, K. Mueller, "Visual Correlation Analysis of Numerical and Categorical Data on the Correlation Map," IEEE Trans. on Visualization and Computer Graphics, 21(2): 289-303, 2015. ppt pdf.