Geometric Optimal Transportation Map

Optimal mass transportation map transforms one measure to the other in the most economic way. It has broad applications in deep learning, computer graphics, computer vision, medical imaging and geometric modeling. In 2013, We developed a variational theoretic framework for semi-discrete optimal mass transportation, which converts solving the optimal mass transportation problem to the optimization of a convex energy, furthermore it gives the explicit geometric interpretation to the convex energy, and the geometric interpretation to the Hessian matrix. This theoretic article can be found here . The talk slides given in IPAM UCLA on Feburaray 12, 2016 can be found here. Geoemtric optimal transportation algorithm can be used in GAN models to eliminate mode collapsing and mode mixture, a talk given in ICCV 2019 can be found here.

Geometric Optimal Transportation Map for Surface Parameterizations

3D surfaces are conformally mapped on the unit disk by a Riemann mapping, then the conformal factor is treated as a probability density function, the optimal transportation map to the uniform distribution is calculated using the geometric OT algorithm. The left frame is the original 3D surface, the middle frame is the Riemann mapping result, the right frame is the image of the optimal transportation map.
buddaha
Alex

Brenier Optimal Transportation Theorem/Alexandrov Convex Polytope Theorem

The algorithm is based on the classical Brenier optimal transportation theorem, which claims that the optimal transportation map is the gradient of a convex function, the so-called Brenier potential. This is equivalent to the Alexandrov theorem in convex geometry, which claims that a convex polytope is uniquely determined by the facet normals and volumes. Gu-Luo-Sun-Yau's theorem gives a variational approach to compute the Brenier potential, equivalently the Alexandrov's polytope. The algorithm computes explicitly the Brenier potential and its Legendre dual using computational geometric methods.
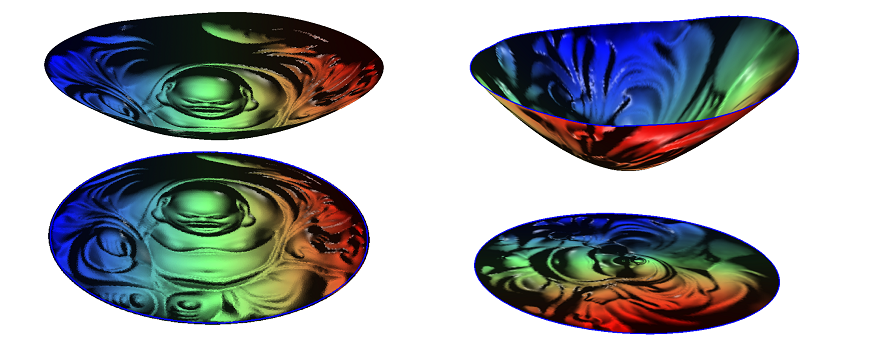
Sophie
The left frame shows the Breiner potential, the right frame shows the Legendre dual of the Brenier potential. The projection of the Brenier potential gives a power diagram, the projection of the Legendre dual gives a power Delaunay triangulation. The power Delaunay triangulation is computed using Lawson's edge flipping for power Delaunay triangulation, the power cell clipping is based on Sutherland-Hodgman convex polygon clipping algorithm. Alternatively one can use incremental convex hull algorithm, and Bentley-Ottman sweep line algorithm to compute as well.

Worest Transportation Map

The same algorithm can be applied for computing the worst transportation map, which maps one probability measure to another one in the least economical way. The mapping is the gradient of a strictly concave function.
Sophie
The left frame is the source measure, the middle frame is the image of the optimal transportaiton map, the right frame is the image of the worst transportation map.
Sophie
The left frame is the Brenier potential for the optimal transportation map, whereas the right frame for the worst transportation map.

Computational Process

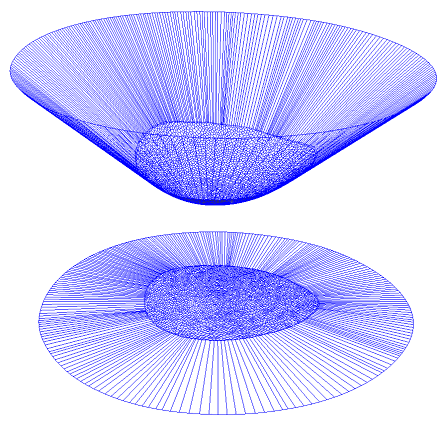
input
Step One Input the source and target probabillity measures and their support sets. The left is the target mesh, represented as a triangle mesh, each vertex represents a sampling point, the planar position of the vertex is defined by the vertex uv coordinates, the target measure of the vertex is also specified. In our demo source code, we conformally map the 3D surface onto the planar disk using a Riemann mapping, the Riemann mapping pushes forward the surface area element to the disk. We use the push-forwarded measure as the target measure. In practice, users and define the vertex target measure in different ways. The source mesh is a strictly convex planar domain as shown in the right frame.
input
Step Two Compute the convex hull (Legendre dual of the brenier potential), or equivalently compute the power Delaunay triangulation using Lawson's edge flip algorithm. If there is an edge, which is not local power Delaunay, but not flippable, then it means some samples are not on the convex hull, hence the algorithm exceeds the admissible space.
input
Step Three Compute the upper envelop (Brenier potential). We add an infinity vertex above all vertices, representing the horizontal plane with very big height, and compute the dual vertex of each face, dual face of each vertex, and dual edge of each edge.
input
Step Four Clip the power cells using Sutherland-Hodgman algorithm, or Bentley-Ottman sweepline algorithm. If some power cells are empty, then the algorithm exceeds the admissible space, then we reduce the step length by half to retreat to the admissible space.
input
Step Five Compupte the power cell areas, which give the gradient of the energy. Compute the power Delaunay edge lengths and the power Vornoi edge lengths, which gives the Hessian matrix of the energy. Use Newton's method to compute the update direction for the vertex powers. Repeat step two through five, until the gradient is close to zero. The figure shows the optimization process, the mappings converge to the unique optimal transportation map.

Comannd Line

OT.exe -source < source mesh > -target <taraget mesh> [option] the following options are supported:
-source <source mesh> the source convex planar domain
-target <target mesh> the target domain and the measure
-step_length <step length> set the step length, ie 0.05
-help show the help message!

Examples: OT.exe -nearest -source disk.obj -target alex.obj -step_length 0.5

Hot Keys

OT.exe hot keys the following options are supported:
'!' Use Newton's method to update one step
'd' show convex hull or upper envelope, Delaunay triangulation or Power Diagram
'g' show 3D view or 2D view
'l' show power cell boundaries
'c' show power cell centers
'e' show edges
'o' take a snapshot
'L' change light source position
'?' Help information
'W' output the Legendre dual mesh and the optimal transportation map mesh

The viewer uses arcball interface, press the left mouse button and drag for rotation, press the right mouse button and drag for zoom in or out, press the middle mouse button and drag for translation.

Download and Instructions

Environment and Dependencies

  1. The OT mapper is developed using generic C++ language on Windows Visual Studio. It has been tested on Linux platforms as well.
  2. It uses freeglut for 3D rendering and GUI.
  3. It uses Eigen for numerical computation;
  4. It uses Shewchuk's adaptive robust predicates package for computational geometry.
  5. You can use cmake for compilation.

References

For any further information, comments and criticisms, please contact David Gu.