Public Member Functions | Protected Member Functions | Protected Attributes

MeshLib::CSparseMatrix Class Reference

CSparseMatrix. More...

#include <SparseMatrix.h>

Collaboration diagram for MeshLib::CSparseMatrix:
Collaboration graph
[legend]

List of all members.

Public Member Functions

 CSparseMatrix (int nRows, int nCols, int nnz=0)
void AddElement (int nRow, int nCol, double dVal)
void AddElementTail (int nRow, int nCol, double dVal)
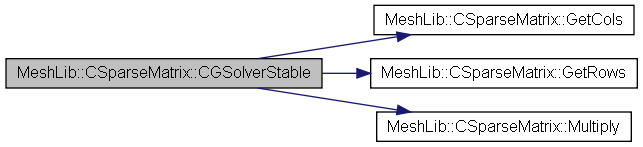
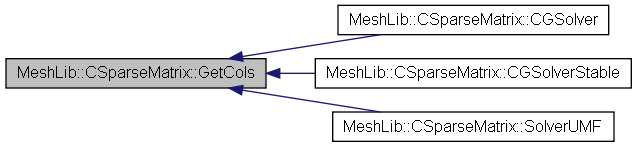
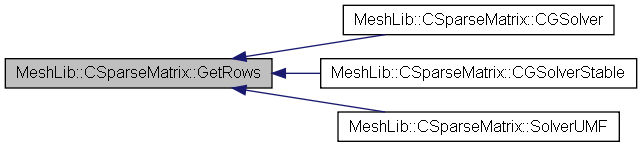
bool CGSolver (double b[], double x[], double eps, int &itrs)
bool CGSolverStable (double b[], double x[], double eps, int &itrs)
bool SolverUMF (double b[], double x[])
void Multiply (double iVector[], double oVector[])
void TransMul (double iVector[], double oVector[])
int GetCols ()
int GetRows ()
virtual ~CSparseMatrix ()

Protected Member Functions

int CalcHashCode (int nRow, int nCol)

Protected Attributes

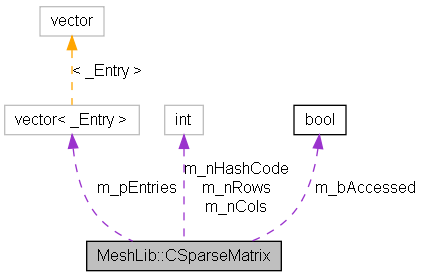
int m_nRows
int m_nCols
bool * m_bAccessed
int m_nHashCode
vector< _Entry > * m_pEntries

Detailed Description

CSparseMatrix.

Sparse matrix entries are organized in an array. Matrix vector multiplication, linear system solver are implemented. The major application of this class is to solve linear system

\[ Ax = b. \]

In most cases, the matrix is symmetric positive definite.

Definition at line 44 of file SparseMatrix.h.

Constructor & Destructor Documentation

CSparseMatrix::CSparseMatrix ( int  nRows,
int  nCols,
int  nnz = 0 
)

CSparseMatrix constructor

Parameters:
nRows number of rows
nCols number of columns
nnz hint for the number of entries

CSparsematrix constructor

Parameters:
nRows number of rows
nCols number of columns
nnz estimated number of non-zeros

Definition at line 39 of file SparseMatrix.cpp.

{
        m_nRows = nRows;
        m_nCols = nCols;
        assert(nRows > 0);
        assert(nCols > 0);
        m_pEntries = new vector<_Entry>();
        if (nnz > 0)
                m_pEntries->reserve(nnz);

        if (nnz > 1024)
        {
                m_nHashCode = nnz;
        }
        else
        {
                m_nHashCode = (nRows > nCols)? nRows * 6: nCols * 6;
        }

        // prime will be better
        if (m_nHashCode % 2 == 0)
                m_nHashCode++;

        m_bAccessed = new bool[m_nHashCode];
        memset(m_bAccessed, 0, sizeof(bool) * m_nHashCode);
}

CSparseMatrix::~CSparseMatrix (  )  [virtual]

virtual CSparseMatrix destructor

CSparsematrix destructor

Definition at line 70 of file SparseMatrix.cpp.

{
        if (m_pEntries != NULL)
                delete m_pEntries;

        delete [] m_bAccessed;
}

Member Function Documentation

void CSparseMatrix::AddElement ( int  nRow,
int  nCol,
double  dVal 
)

Add an element to the matrix,

Parameters:
nRow row position
nCol col position
dVal the value of the entry

Add element, checking duplicacy using Hash table

Parameters:
nRow row position
nCol col position
dVal value of the entry

Definition at line 95 of file SparseMatrix.cpp.

{
        _Entry entry;
        assert(nRow >= 0 && nRow < m_nRows);
        assert(nCol >= 0 && nCol < m_nCols);
        bool bFound = false;
        
        int hash = CalcHashCode(nRow, nCol);
        if (m_bAccessed[hash])
        {
                for (int i = 0; i < (int)m_pEntries->size(); i++)
                {
                        _Entry& e = m_pEntries->at(i);
                        if (e.i == nRow && e.j == nCol)
                        {
                                e.val += dVal;
                                if (isZero(e.val))
                                {
                                        if (m_pEntries->size() > 0)     // Copy last to current
                                        {
                                                m_pEntries->at(i) = m_pEntries->at(m_pEntries->size() - 1);
                                        }
                                        m_pEntries->resize(m_pEntries->size() - 1);
                                }
                                bFound = true;
                                break;
                        }
                }
        }
        if (!bFound)
        {
                m_bAccessed[hash] = true;
                entry.i = nRow;
                entry.j = nCol;
                entry.val = dVal;
                m_pEntries->push_back(entry);
        }
}

Here is the call graph for this function:

void CSparseMatrix::AddElementTail ( int  nRow,
int  nCol,
double  dVal 
)

Add an element to the matrix,

Parameters:
nRow row position
nCol col position
dVal the value of the entry

Add element to the tail, without check duplicacy

Parameters:
nRow row position
nCol col position
dVal value of the entry

Definition at line 141 of file SparseMatrix.cpp.

{
        _Entry entry;
        assert(nRow >= 0 && nRow < m_nRows);
        assert(nCol >= 0 && nCol < m_nCols);

        entry.i = nRow;
        entry.j = nCol;
        entry.val = dVal;
        m_bAccessed[CalcHashCode(nRow, nCol)] = true;

        m_pEntries->push_back(entry);
//      printf("(%d,%d) %f\n", nRow, nCol, dVal);
}

Here is the call graph for this function:

int CSparseMatrix::CalcHashCode ( int  nRow,
int  nCol 
) [protected]

Calculate Hash code

Parameters:
nRow number of rows
nCol number of columns

Compute Hash code

Parameters:
nRow row position
nCol col position
Returns:
Hash value

Definition at line 84 of file SparseMatrix.cpp.

{
        return (nRow * 37 + nCol * 103) % m_nHashCode;
}

Here is the caller graph for this function:

bool CSparseMatrix::CGSolver ( double  b[],
double  x[],
double  eps,
int &  itrs 
)

Conjugate gradient solver to solve Ax = b

Parameters:
b known vector
x unknown vector
eps error tolerance
itrs number of iterations

Conjugate Gradient Solver to solve the linear system Ax = b

Parameters:
b known vector
x unkown vector
eps error tolerance
itrs iterations

Definition at line 162 of file SparseMatrix.cpp.

{
        if( GetRows()!=GetCols() )
                return false;

        int size = this->GetRows();
        // initialize
        double alpha, beta;
        double* r = new double[size];
        double* p = new double[size];
        double* temp = new double[size];
        double* multi = new double[size];
        assert( r != NULL && p != NULL && temp != NULL && multi != NULL );

        // x_0 = b_0
        for( int i=0; i<size; i++ )
                x[i] = b[i];

        // r_0 = b - A*x_0
    Multiply( x, multi );
        
        //spM->TimesVDirect( x, size, multi, size );

        for( int i=0; i<size; i++ )
                r[i] = b[i] - multi[i];

        //for( int i=0; i<size; i++ )
        //x[i] = multi[i];
        //  p_1 = r_0
        for( int i=0; i<size; i++ )
                p[i] = r[i];

        double numerator, denominator;

        int step = 0;

        double norm_b = 0.0;
        for( int i=0; i<size; i++ )
                norm_b += b[i]*b[i];
        norm_b = sqrt( norm_b );

        double norm_r = 0.0;

        while( true )
        {
                if( itrs>=0 )
                        if( step>=itrs )
                                break;
                // ||r||/||b|| < threshold, then break
                norm_r = 0.0;
                for( int i=0; i<size; i++ )
                        norm_r += r[i]*r[i];
                norm_r = sqrt( norm_r );

                if( norm_r/norm_b<eps )
                        break;

                // \alpha_k = r_{k-1}^T*r_{k-1}/p_k^T(A*p_k) 
                numerator = 0.0;
                for( int i=0; i<size; i++ )
                        numerator += r[i]*r[i];


                //spM->TimesVDirect( p, size, multi, size );
                this->Multiply( p, multi );

                denominator = 0.0;
                for( int i=0; i<size; i++ )
                        denominator += p[i]*multi[i];

                alpha = numerator/denominator;

                // x_k = x_{k-1} + \alpha_k * p_k
                for( int i=0; i<size; i++ )
                        x[i] = x[i] + alpha*p[i];

                for( int i=0; i<size; i++ )
                        temp[i] = r[i];         // temp ---- r_{k-1}

                // r_k = r_{k-1} - \alpha_k*(A*p_k)
                for( int i=0; i<size; i++ )
                        r[i] = temp[i] - alpha*multi[i];

                // \beta = r_k^T*r_k/(r_{k-1}^T*r_{k-1})
                numerator = 0.0;
                for( int i=0; i<size; i++ )
                        numerator += r[i]*r[i];
                denominator = 0.0;
                for( int i=0; i<size; i++ )
                        denominator += temp[i]*temp[i];
                beta = numerator/denominator;

                // p_{k+1} = r_k + \beta*p_k
                for( int i=0; i<size; i++ )
                        p[i] = r[i]+beta*p[i];

                step++;
        }

        //spM->TimesVDirect( x, size, multi, size );
        this->Multiply( x, multi );

        double sum = 0.0;
        for( int i=0; i<size; i++ )
                sum += (multi[i]-b[i])*(multi[i]-b[i]);
        sum = sqrt( sum );

        
        printf( "CG iter_num: %d error: %.10f\n", step, norm_r/norm_b );

        delete []r;
        delete []p;
        delete []multi;
        delete []temp;

        return true;
}

Here is the call graph for this function:

bool CSparseMatrix::CGSolverStable ( double  b[],
double  x[],
double  eps,
int &  itrs 
)

Conjugate gradient solver to solve Ax = b, stabler version

Parameters:
b known vector
x unknown vector
eps error tolerance
itrs number of iterations

Definition at line 393 of file SparseMatrix.cpp.

{
        if( GetRows()!=GetCols() )
                return false;

        int size = this->GetRows();
        // initialize
        double alpha, beta;
        double  sum;
        double* r = new double[size];
        double* p = new double[size];
        double* multi = new double[size];
        double* temp = new double[size];

        // x_0 = b_0
        for( int i=0; i<size; i++ )
                x[i] = b[i];

        // r_0 = b - A*x_0
        sum = 0.0;
        for( int i=0; i<size; i++)
                sum += x[i];
        for( int i=0; i<size; i++ )
        {
                temp[i] = -(sum-x[i]);
        }
        //spM->TimesVDirect( temp, size, multi, size );
        this->Multiply( temp, multi ); 


        sum = 0.0;
        for( int i=0; i<size; i++)
                sum += multi[i];
        for( int i=0; i<size; i++ )
        {
                temp[i] = -(sum-multi[i]);
        }

        for( int i=0; i<size; i++ )
                r[i] = b[i] - temp[i];

        //  p_1 = r_0
        for( int i=0; i<size; i++ )
                p[i] = r[i];

        double numerator, denominator;

        int step = 0;

        double norm_b = 0.0;
        for( int i=0; i<size; i++ )
                norm_b += multi[i]*multi[i];
        norm_b = sqrt( norm_b );

        double norm_r = 0.0;

        while( true )
        {
                if( itrs>=0 )
                        if( step>=itrs )
                                break;
                // ||r||/||b|| < threshold, then break
                norm_r = 0.0;
                for( int i=0; i<size; i++ )
                        norm_r += r[i]*r[i];
                norm_r = sqrt( norm_r );

                if( norm_r/norm_b<eps )
                        break;

                //fprintf( stderr, "%d - norm_r/norm_b = %.10f\n", step, norm_r/norm_b );

                // \alpha_k = r_{k-1}^T*r_{k-1}/p_k^T(A*p_k) 

                numerator = 0.0;
                for( int i=0; i<size; i++ )
                        numerator += r[i]*r[i];

                sum = 0.0;
                for( int i=0; i<size; i++ )
                        sum += p[i];
                for( int i=0; i<size; i++ )
                {
                        temp[i] = -(sum-p[i]);
                }
                //spM->TimesVDirect( temp, size, multi, size );
                this->Multiply( temp, multi );
                sum = 0.0;
                for( int i=0; i<size; i++ )
                        sum += multi[i];
                for( int i=0; i<size; i++ )
                {
                        temp[i] = -(sum-multi[i]);
                }               // temp --- A*p_k

                denominator = 0.0;
                for( int i=0; i<size; i++ )
                        denominator += p[i]*temp[i];

                alpha = numerator/denominator;

                // x_k = x_{k-1} + \alpha_k * p_k
                for( int i=0; i<size; i++ )
                        x[i] = x[i] + alpha*p[i];

                for( int i=0; i<size; i++ )
                        multi[i] = r[i];                // multi ---- r_{k-1}

                // r_k = r_{k-1} - \alpha_k*(A*p_k)
                for( int i=0; i<size; i++ )
                        r[i] = multi[i] - alpha*temp[i];

                // \beta = r_k^T*r_k/(r_{k-1}^T*r_{k-1})
                numerator = 0.0;
                for( int i=0; i<size; i++ )
                        numerator += r[i]*r[i];
                denominator = 0.0;
                for( int i=0; i<size; i++ )
                        denominator += multi[i]*multi[i];
                beta = numerator/denominator;

                // p_{k+1} = r_k + \beta*p_k
                for( int i=0; i<size; i++ )
                        p[i] = r[i]+beta*p[i];

                step++;
        }


        //printf( "CG iter_num: %d error: %.10f\n", step, norm_r/norm_b );

        delete []r;
        delete []p;
        delete []temp;
        delete []multi;

        return true;
}

Here is the call graph for this function:

int MeshLib::CSparseMatrix::GetCols (  )  [inline]

Get number of columns

Definition at line 134 of file SparseMatrix.h.

        {
                return m_nCols;
        }

Here is the caller graph for this function:

int MeshLib::CSparseMatrix::GetRows (  )  [inline]

Get number of rows

Definition at line 141 of file SparseMatrix.h.

        {
                return m_nRows;
        }

Here is the caller graph for this function:

void CSparseMatrix::Multiply ( double  iVector[],
double  oVector[] 
)

Matrix, vector multiplication

Parameters:
iVector input vector
oVector output vector
Returns:
oVector = A iVector

Definition at line 286 of file SparseMatrix.cpp.

{
        memset(oVector, 0, sizeof(double) *     m_nRows);
        for (int i = 0; i < (int)m_pEntries->size(); i++)
        {
                _Entry& entry = m_pEntries->at(i);
                oVector[entry.i] += iVector[entry.j] * entry.val;
        }
}

Here is the caller graph for this function:

bool CSparseMatrix::SolverUMF ( double  b[],
double  x[] 
)

Solve linear system Ax = b, using UMF

Parameters:
b known vector
x unknown vector

Definition at line 544 of file SparseMatrix.cpp.

{
        std::sort( (*m_pEntries).begin(), (*m_pEntries).end(), Predicate );


        int n = m_pEntries->size();
/*
        for( int i = 0; i < n ; i ++ )
        {
                _Entry & e = m_pEntries->at(i);
                printf("(%d %d)\n", e.i, e.j);
        }
*/

        int *Ai = new int[n];
        double *Ax = new double[n];

        for( int i = 0; i < n ; i ++ )
        {
                _Entry & e = m_pEntries->at(i);
                Ai[i] = e.i;
                Ax[i] = e.val;
        }

        int row = GetRows();
        int col = GetCols();


        int *Ap = new int[col+1];

        for( int i = 0; i < col + 1; i ++ )
        {
                Ap[i] = 0;
        }

        for( int i = 0; i < n ; i ++ )
        {
                _Entry & e = m_pEntries->at(i);
                Ap[e.j+1]++;
        }

        for( int i = 1; i < col + 1; i ++ )
        {
                Ap[i] = Ap[i] + Ap[i-1];
        }

        printf("%d - %d\n", Ap[col], n );

        void *Symbolic, *Numeric ;
        double *null = (double *) NULL ;
        (void) umfpack_di_symbolic (row, col, Ap, Ai, Ax, &Symbolic, null, null) ;
        (void) umfpack_di_numeric (Ap, Ai, Ax, Symbolic, &Numeric, null, null) ;
        umfpack_di_free_symbolic (&Symbolic) ;
        (void) umfpack_di_solve (UMFPACK_A, Ap, Ai, Ax, x, b, Numeric, null, null) ;
        umfpack_di_free_numeric (&Numeric) ;

        delete []Ap;
        delete []Ax;
        delete []Ai;

        return true;
}

Here is the call graph for this function:

void CSparseMatrix::TransMul ( double  iVector[],
double  oVector[] 
)

Transposed Matrix, vector multiplication

Parameters:
iVector input vector
oVector output vector
Returns:
oVector = A^T iVector

Definition at line 300 of file SparseMatrix.cpp.

{
        memset(oVector, 0, sizeof(double) * m_nCols);
        for (int i = 0; i < (int)m_pEntries->size(); i++)
        {
                _Entry& entry = m_pEntries->at(i);
                oVector[entry.j] += iVector[entry.i] * entry.val;
        }
}

Member Data Documentation

bool* MeshLib::CSparseMatrix::m_bAccessed [protected]

data structurre for Hash code

Definition at line 59 of file SparseMatrix.h.

int MeshLib::CSparseMatrix::m_nCols [protected]

number of columns of the matrix

Definition at line 54 of file SparseMatrix.h.

int MeshLib::CSparseMatrix::m_nHashCode [protected]

Definition at line 60 of file SparseMatrix.h.

int MeshLib::CSparseMatrix::m_nRows [protected]

number of rows of the matrix

Definition at line 50 of file SparseMatrix.h.

vector<_Entry>* MeshLib::CSparseMatrix::m_pEntries [protected]

array of entries

Definition at line 65 of file SparseMatrix.h.

The documentation for this class was generated from the following files:
 All Classes Namespaces Files Functions Variables Typedefs Enumerator Defines
Generated on Sun Oct 31 2010 21:37:47 for RiemannMappingLibrary by  doxygen 1.7.1