Vandegriend's Finding Hamiltonian Cycles
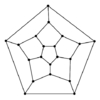
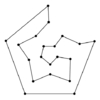
From his abstract:My Master's thesis "Finding Hamiltonian Cycles: Algorithms, Graphs and Performance" deals with the Hamiltonian cycle problem, an NP-C problem in graph theory. The problem consists of finding a tour (or cycle) that visits all the vertices once and returns to the starting vertex. I have investigated several related issues:
* Design issues for backtrack Hamiltonian cycle algorithms
* Design issues for heuristic Hamiltonian cycle algorithms
* Generalizations of the knight's tour problem (a subset of the Hamiltonian cycle problem).
* Hard regions of the Hamiltonian cycle problem. My goal here is to identify graphs and graph properties that make the Hamiltonian cycle problem hard or that distinguish between various Hamiltonian cycle algorithms. I have focused mainly on low degree randomized graphs.
Download Files (local site)Offical Site
Problem Links
This page last modified on 2008-07-10
.
www.algorist.com