Eulerian Cycle Animation
An Eulerian cycle in a graph is a traversal of all the edges of the graph that visits each edge exactly once before returning home. The problem was made famous by the bridges of Konigsberg, where a tour that walked on each bridge exactly once was unsuccessfully sought.

A graph has an Eulerian cycle if and only if all its vertices are that of even degrees. To actually find such a tour, we can extact cycles from the graph and then graft them together, noting that the deletion of cycle must leave even degree vertices as even.

It is amusing to watch as the Eulerian cycle finds a way back home to a seemingly blocked off start vertex. We are allowed (indeed required) to visit vertices multiple times in an Eulerian cycle, but not edges.

Download:

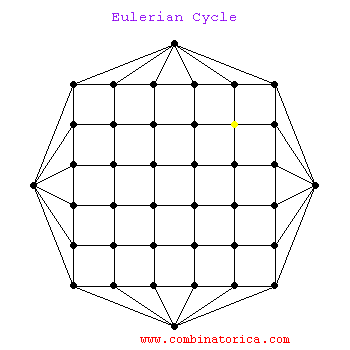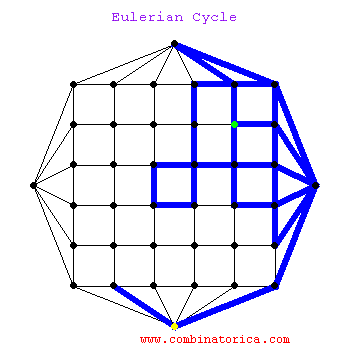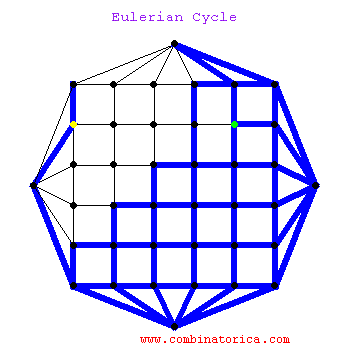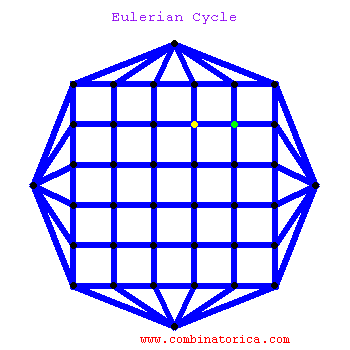
  euler.gif - The Animation.
  euler.nb - Notebook file.

These animations were produced using Combinatorica -- see www.combinatorica.com and our book Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica for more information.

Check out our dfs/bfs, connected components, Hamiltonian cycle, Eulerian cycle, shortest path, transitive closure, and minimum spanning tree animations!