1.3.10 Satisfiability
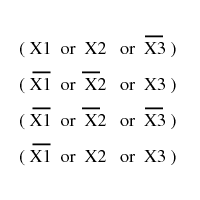

INPUT OUTPUT
Input Description:
A set of clauses in conjunctive normal form.
Problem:
Is there a truth assignment to the boolean variables
such that every clause is satisfied?
Excerpt from
The Algorithm Design Manual:
Satisfiability arises whenever we seek a configuration or object that must be consistent with (\ie satisfy) a
given set of constraints. For example, consider the problem of drawing name labels for cities on a map. For
the labels to be legible, we do not want the labels to overlap, but in a densely populated region many labels
need to be drawn in a small space. How can we avoid collisions?
For each of the n cities, suppose we identify two possible places to position its label, say right
above or right below each city. We can represent this choice by a Boolean variable vi,
which will be true if city ci's label is above ci, otherwise
vi = false. Certain pairs of labels may be forbidden, such as when ci's
above label would obscure cj's below label. This pairing can be forbidden by the two-element
clause $(\bar{v_i} \OR v_j )$, where $\bar{v}$ means ``not $v$''. Finding a satisfying truth assignment for
the resulting set of clauses yields a mutually legible map labeling if one exists.
Satisfiability is the original NP-complete problem. Despite its applications to constraint
satisfaction, logic, and automatic theorem proving, it is perhaps most important theoretically as the root
problem from which all other NP-completeness proofs originate.
Recommended Books
Related Links
SAT Live! up-to-date source for papers, programs, and test sets for satisfiability and related logic optimization problems
Reactive Search, a History-Sensitive Heuristic for Max-Sat by R. Battiti and M. Protasi
9th International Conference on Theory and Applications of Satisfiability Testing
Journal on Satisfiability, Boolean Modeling and Computation
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com


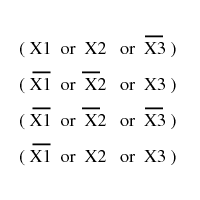

 Satisfiability Testing
Satisfiability Testing Algorithm Design
Algorithm Design Introduction to Algorithms
Introduction to Algorithms Computers and Intractability: A Guide to the Theory of NP-Completeness
Computers and Intractability: A Guide to the Theory of NP-Completeness