About the Book

The Stony Brook Algorithm Repository

Steven Skiena
Stony Brook University
Dept. of Computer Science

1.6.1 Robust Geometric Primitives

INPUT                    OUTPUT

Input Description: A point $p$ and a line segment $l$, or two line segments $l_1$ and $l_2$.

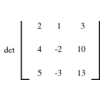
Problem: Does $p$ lie over, under, or on $l$? Does $l_1$ intersect $l_2$?

Excerpt from The Algorithm Design Manual: Implementing basic geometric primitives is a task fraught with peril, even for such simple tasks as returning the intersection point of two lines. What should you return if the two lines are parallel, meaning they don't intersect at all? What if the lines are identical, so the intersection is not a point but the entire line?

What if one of the lines is horizontal, so that in the course of solving the equations for the intersection point you are likely to divide by zero? What if the two lines are almost parallel, so that the intersection point is so far from the origin as to cause arithmetic overflows? These issues become even more complicated for intersecting line segments, since there are a bunch of other special cases that must be watched for and treated specially.