1.6.15 Maintaining Line Arrangements
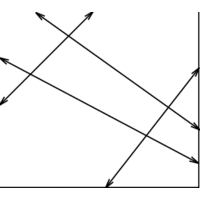
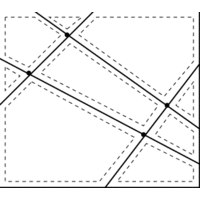
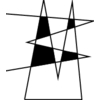
INPUT OUTPUT
Input Description:
A set of lines and line segments l_1,...,\l_n.
Problem:
What is the decomposition of the plane defined by l_1,...,\l_n?
Excerpt from
The Algorithm Design Manual:
One of the most fundamental problems in computational geometry
is constructing arrangements of lines, that is, explicitly
building the regions formed by the intersections of a set of $n$ lines.
Algorithms for a surprising number of problems are based on constructing
and analyzing the arrangement of a specific set of lines:
- Degeneracy testing -- Given a set of $n$ lines in the plane,
do any three of them pass through the same point?
Brute-force testing of all triples takes O(n3) time.
Instead, we can construct the arrangement of the lines and then
walk over each vertex and explicitly count its degree,
all in quadratic time.
- Satisfying the maximum number of linear constraints --
Suppose that we are given a set of $n$ linear constraints, each of the
form y less and or equal to ai x + bi.
Which point in the plane satisfies the largest number of them?
Construct the arrangement of the lines.
All points in any region or cell
of this arrangement satisfy exactly the same
set of constraints, so we need to test only one point per cell in order
to find the global maximum.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Davenport-Schinzel sequences and their geometric applications
Computational Geometry in C
Algorithms in Combinatorial Geometry
