CSE 691 - Lecture 13 - Spectral Analysis

Steven S. Skiena

Dept. of Computer Science

SUNY Stony Brook

Spectral Analysis

Certain phenomena of financial (and other) time series data is best revealed in the frequency domain, or equivalently represented by their spectra.

A duality transform is a one-to-one mathematical function that takes a mathematical object of type-1 and maps it to an equivalent type-2 mathematical object.

Sample duality relations are point-line duality in computational geometry, and Laplace transforms used solving differential equations.

Such transforms are useful if there are interesting algorithms and tools for manipulating data of type 2.

Perhaps the most useful duality transform known is the Fourier transform for representing time-series data as the sums of sine and cosine functions.

Its wide applicability is due to the existence of Fast Fourier Transform algorithm or FFT which computes what seems like an inherently quadratic function in $O(n \lg n)$ time.

Filtering via the FFT

On the left, we construct a time series of points sampled from a sine function with added random noise.

On the right we take the Fourier transform of this series, plotting the coefficients of the resulting sine functions:

figure=figures/fourier-transform-L.eps,width=3.5in figure=figures/fourier-transform-R.eps,width=3.5in

• Filtering - By eliminating undesirable high- and/or low-frequency components (i.e. dropping some of the sine functions) and taking an inverse Fourier transform to get us back into the time domain, we can filter a function to remove noise and other artifacts.

• Compression - A smoothed function less information than a noisy function, while retaining a similar appearance. We can perform lossy compression by eliminating the coefficients of sine functions that contribute relatively little to the function.

FFT Filtering Example

Note how very particular cross-hatching was removed by eliminating the appropriate transform coefficients.

figure=figures/fft-example.eps,width=5.0in

Convolutions and Correlation

• Convolution and Deconvolution - A convolution is the pairwise product of elements from two different sequences, such as in multiplying two $n$-variable polynomials $f$ and $g$ or multiplying two long integers. Implementing the product directly takes $O(n^2)$, while $O(n \lg n)$ suffices using the fast Fourier transform.

• Computing the correlation of functions - The correlation function of two functions $f(t)$ and $g(t)$ is defined by
  
  $$z(t) = \int_{-\infty}^{\infty} f(\tau) g(t + \tau)$$
  
  
  and can be easily computed using Fourier transforms.

  If the two functions are similar in shape but one is shifted relative to the other (such as $f(t) = \sin(t)$ and $g(t) = \cos(t)$), the value of $z(t_0)$ will be large at this shift offset $t_0$.

  As an application, suppose that we want to detect whether there are any funny periodicities (autocorrelations) in a time series or random number generator. When we take the Fourier transform of this series, any large spikes will correspond to potential periodicities.

Polynomials: A Refresher

We can represent a given polynomial

$$A(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_{n_1} x^{n-1}$$

by either (1) the set of coefficients $a_i$, or (2) a set of $n$ points $(x_i,y_i)$ on the polynomial, i.e. $y_i = A(x_i)$.

Given the coefficient representation, we can add or subtract two polynomials in $O(n)$ time by just adding or subtracting each pair of corresponding terms.

Given the coefficient representation, we can evaluate a polynomial in linear time using Horner's rule

$$A(x) = a_0 + x(a_1 + x(a_2 + x(a_3 + \ldots)))$$

It is not clear how to multiply two polynomials in coefficient representation in less than $O(n^2)$.

However, it is easy add, subtract, and multiply pairs of polynomials in point-value representation (assuming the same set of $x_i$ values is used in both polynomials) by operating on the pair of points for each $x$ value.

We can multiply coefficient polynomials by (1) converting them to point-value representation, (2) multiply these pointwise in $O(n)$, and (3) interpolate these $2n$ points back to a polynomial.

Note that the product of two $n$-degree polynomials has degree $2n$.

Steps (1) and (3) can in fact be done on $O(n \log n)$ by using the DFT and inverse transform.

Lagrange's formula can solve the interpolation problem in $O(n^2)$, but it is too slow.

Complex Numbers: A Refresher

Although any polynomial of degree $d$ should have $d$ roots/solutions, they sometimes require complex numbers:

$$x^2 + 1 = 0$$

If $i = \sqrt{-1}$, the two solutions are $i$ and $-i$.

The $n$ roots of unity are the $n$ solutions to the equation

$$x^n = 1$$

These roots are defined by the $n$ powers $\omega_n^i$ for $0 \leq i \leq n-1$, where

$$\omega_n = \cos(2 \pi / n) + i \sin(2 \pi / n) = e^{2 \pi i / n}$$

The identity linking the trigonometric functions to $e$ is

$$e^{i u} = \cos u + i \sin u$$

The Discrete Fourier Transform

The discrete Fourier transform takes as input $n$ complex numbers $h_k$, $0 \leq k \leq n-1$, corresponding to equally spaced points in a time series.

It outputs $n$ complex numbers $H_k$, $0 \leq k \leq n-1$, each describing a trigonometric function of the given frequency.

The discrete Fourier transform is defined by

$$H_m = \sum_{k=0}^{n-1} h_k e^{-2 \pi i k m / n}$$

and the inverse Fourier transform is defined by

$$h_m = \frac{1}{n} \sum_{k=0}^{n-1} H_k e^{2 \pi i k m / n}$$

which enables us move easily between $h$ and $H$.

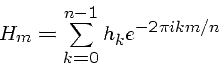
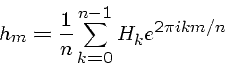
However, the complexity of a naive implementation is $O(n^2)$.

The FFT Algorithm

The critical step in efficiently computing the DFT takes as input a set of $n$ complex numbers $a_0, a_1, \ldots, a_{n-1}$ and outputs the sequence of $n$ complex numbers

$$A(1), A({\omega_n}^1), A({\omega_n}^2), \ldots, A({\omega_n}^{n-1})$$

resulting from evaluating the polynomial

$$A(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_{n_1} x^{n-1}$$

In particular, to evaluate $A(x)$ when $n$ is even, let

$$A_{even}(y) = a_0 + a_2 y + \ldots + a_{n-2} y^{n/2-1}$$

$$A_{odd}(y) = a_1 + a_3 y + \ldots + a_{n-1} y^{n/2-1}$$

It should be clear that

$$A_(x) = A_{even}(x^2) + x A_{odd}(x^2)$$

FFT algorithms are based on divide-and-conquer. Essentially, the problem of computing the discrete Fourier transform on $n$ points is reduced to computing two transforms on $n/2$ points each and is then applied recursively.

In general, this recurrence does not help us, since we have to spend linear time to evaluate it at each of $n$ points. The fact that our points are complex roots of unity provide the magic to speed things up.

Implementation Details

The FFT algorithm assumes that $n$ is a power of two.

If this is not the case for your data, you are better off padding your data with zeros to create $n=2^k$ elements rather than hunting for a more general code.

Some care is needed to determine where to best pad the zeros.

Historically, the FFT has been implemented in assembler or even hardware for performance optimization.

Highly optimized FFT implementation exist which tune themselves to your specific hardware configurations (e.g. cache size). Check out the FFTW (Fastest Fourier Transform in the West).

In recent years, wavelets have been proposed to replace Fourier transforms in filtering.