

Next: About this document ...
Up: My Home Page
Administrivia
Make sure I get your name and email address written clearly,
as well as whether you intend to take this course for credit.
I need volunteers particularly for the first presentation, one week from today.
Do I have any volunteers to help index and digitize the lecture audio?
Project lists should go out in a few weeks.
Why Computational Biology?
Computational biology is the application of a core technology
of computer science (e.g. algorithms, artificial intelligence,
data bases)
to problems arising from biology.
Computational biology is particularly exciting today
because (1) the problems are large enough to motivate efficient
algorithms,
(2) the problems are accessible, fresh and interesting,
(3) biology is increasing becoming a computational science.
Developments in biology are coming astonishingly quickly,
and with amazing possibilities.
Computational biology is increasing of interest in both life science
and computational science departments.
Many problem ideas go from biology to CS:
e.g. fragment assembly, sequence analysis,
algorithms for phylogenic trees.
Many problem ideas go from CS to biology:
e.g. sequencing by hybridization, DNA computing.
Attack on the SARS Virus
The scientific reaction to the outbreak of the SARS virus after being first
reported in Asia in February 2003 illustrates the
critical roles that genomics and computation play in modern biology.
DeRisi's analysis of microarray data reveals that the agent was a coronavirus in March 2003.
The Michael Smith Genome Sciences Centre in Canada announce the sequencing of the SARS
virus genome on April 12, 2003.
Commercial SARS-specific microarrays become available in April 15, 2003.
Gene predictions and analysis of SARS genome published in Science online May 1, 2003.
Phylogenic analysis placing where SARS fits among the coronaviruses published in late May 2003.
We will study the computational problems of sequence assembly, gene prediction, microarray design/analysis,
and phylogenic tree construction in this course.
Computer Scientists vs. Biologists
There are many different types of life scientists (biologists,
ecologists, medical doctors, etc.), just as there are many
different types of computational scientists (algorists, software engineers,
statisticians, etc.).
There are many fundamental cultural differences between
computational/life scientists:
- Nothing is ever completely true or false in biology,
where everything is either true or false in computer science /
mathematics.
- Biologists strive to understand the very complicated, very messy natural world;
computer scientists seek to build their own clean and organized virtual
worlds.
- Biologists are data driven; while computer scientists are
algorithm driven.
One consequence is CS WWW pages have fancier graphics while
Biology WWW pages have more content.
- Biologists are much more obsessed with being the first to discover
something; computer scientists invent more than discover.
- Research biologists have to know more than computer scientists;
computer scientists know how to do more.
- Biologists are comfortable with the idea that all data has errors;
computer scientists are not.
- Biologists are live in stronger hierarchies than computer scientists:
PI
 postdocs
postdocs  graduate students
graduate students  lab assistants.
lab assistants.
Genetics students seeking to work with me ask to join the ``Skiena lab''.
- The Platonic ideal of a biologist runs a big laboratories with many people.
The Platonic ideal of a computer scientists is a hacker in garage.
Biologists can get/spend infinitely more research money than computational
scientists.
- Biotechnology/drug companies are largely science driven,
while the computer industry is more engineering/marketing driven.
- Biologists seek to publish in prestigious journals like
Science and Nature.
Computer scientists seek to publish in prestigious refereed conference
proceedings.
One consequence is life science journals get refereed faster than
computational science journals.
- Computer scientists can get interesting, high-paid jobs after a B.S.
Biologists typically need to complete one or more postdocs...
Biology for Computer Scientists
DNA sequences can be thought of as strings of bases on a four-letter alphabet,
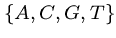 .
.
Each base binds with its complement, 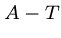 and
and 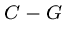 , so each sequence has
a unique complementary sequence.
, so each sequence has
a unique complementary sequence.
The human genome is approximately 3 billion base-pairs long,
and contains all the information necessary to make all the proteins
which you are made of.
Proteins are sequences of amino acids, and hence all proteins can be
thought of as strings on a 20-letter alphabet.
A gene is a DNA sequence which acts as
a template for building a specific protein.
Genes specify how to build proteins according to the
triplet code, where
each of the
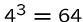 possible sequences or codons of
three consecutive nucleotide bases map to one of the
20 different amino acids or the stop symbol.
possible sequences or codons of
three consecutive nucleotide bases map to one of the
20 different amino acids or the stop symbol.
figure=figures/transcription.eps,width=4in
RNA is an intermediate step in the translation process, and maps 1-to-1
with DNA.
The human genome contains about 50,000 genes, meaning that your body is made
up of about that many different components.
The recently ``completed'' human genome project seeks to sequence
or read the entire set of DNA and protein strings.
But sequencing is just a first step towards understanding what the
proteins do and how to manipulate them.
Only a small portion of the human genome consists of genes.
The rest contains various binding/signaling sites and less
well understood ``junk''.
Organisms
Living organisms differ greatly in complexity and organization.
Viruses are simplest organisms (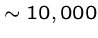 bp. long),
which require a living host.
bp. long),
which require a living host.
Prokaryotes are simplest free-living organisms, e.g. bacteria
(
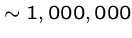 bp. long).
bp. long).
Eukaryotes have cells which contain internal structures
such as a nucleus, e.g. yeast.
Multi-celled organisms involve cell specialization,
requiring differential gene expression and inter-cellular signaling.
Historically, many biologists focused their careers on
one model organism: E. Coli, yeast, drosophila, arabadopsis,
zebrafish, sea urchins, mouse.
The advent of genomics has focused more attention on the similarity
between organisms.
Evolution
Evolutionary change happens because of changes in genomes due
to mutations and recombination.
Mutations are rare events,
sometimes single base changes, sometimes larger events.
Recombination is how your genome was constructed as a mixture
of your two parents.
Through natural selection, favorable changes tend to accumulate in
the genome.
Evolution motivates homology (similarity) search,
because different species are assumed to have common ancestors.
Thus DNA/amino acid sequences for a given protein (e.g. hemoglobin)
in two species or individuals should be more similar the closer the ancestry
between them.
The genetic variation between different people is surprisingly small,
perhaps only 1 in 1000 base-pairs.
Homology searches can often detect similarities between extremely
distant organisms (e.g. humans and yeast).
Phylogenic trees based on gene homologies have provided an
independent confirmation of many phylogenies proposed by taxonomists.
This is convincing evidence of the Theory of Evolution.
A host of interesting computational problems arise in trying to reconstruct
evolutionary history.
Biotechnologies
Amazing biotechnologies for manipulating DNA molecules have been developed,
and are used as building blocks for even more powerful technologies.
These technologies are as amazing to me as the silicon etching/masking
of VLSI fabrication.
DNA synthesis machines enable one to grow short DNA molecules
of a specified sequence.
The Polymerase chain reaction (PCR) enables one to make large number
of copies of a particular DNA sequence anywhere in solution given
only the starting and ending sequences (primers).
PCR is one foundation of DNA fingerprinting,
by turning a single molecule into billions.
Electrophoresis enables one to approximately measure the length
of a DNA molecule, by measuring the time it takes to walk up an electrically
charged Gel.
Since certain regions of the human genome have varying numbers of
repeated characters, measuring their length by electrophoresis yields one
method of DNA fingerprinting / identification.
DNA sequencing machines are built from both these technologies,
and will be discussed when we talk about assembly.
Computer Science for Biologists
We will be interested in the correctness and efficiency of computer
algorithms.
We seek algorithms which provably always return the best possible
solution to a well-defined combinatorial problem.
Heuristics are procedures which might return good answers in
practice, but are not provably correct.
We seek to extract clean, well-defined problems from the typically
messy ``real'' problem to gain insight into it.
This process is analogous to in vitro versus in vivo
experimentation.
Exact String Matching
Input: A text string 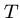 , where
, where 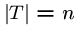 , and a pattern string
, and a pattern string 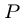 ,
where
,
where 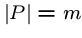 .
.
Output: An index 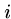 such that
such that
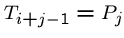 for
all
for
all
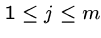 , i.e. showing that
, i.e. showing that 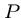 is a substring of
is a substring of 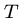 .
.
The following brute force search algorithm always uses at most
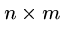 steps:
steps:
for 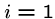 to
to 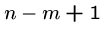 do
do
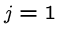
while (![$T[i+j-1] == P[j]$](img24.gif) ) and (
) and ( )
)
do 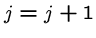
if 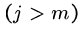 print "pattern at position ",
print "pattern at position ", 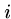
This algorithm might use only 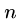 steps if we are lucky, e.g.
steps if we are lucky, e.g.
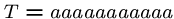 , and
, and 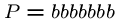 .
.
We might need
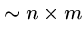 steps if we are unlucky, e.g.
steps if we are unlucky, e.g.
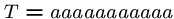 , and
, and 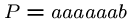 .
.
We can't say what happens ``in practice'', so we settle
for a worst case analysis.
By being more clever, we can reduce the worst case running time to
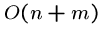 .
.
Certain generalizations won't change this, like stopping after the
first occurrence of the pattern.
Certain other generalizations seem more complicated, like matching with
gaps.
Algorithm Complexity
We use the Big oh notation to state an upper bound on the number of steps
that an algorithm takes in the worst case.
Thus the brute force string matching algorithm is 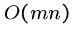 , or takes
quadratic time.
, or takes
quadratic time.
A linear time algorithm, i.e. 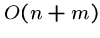 , is fast enough for almost
any application.
, is fast enough for almost
any application.
A quadratic time algorithm is usually fast enough for small problems,
but not big ones, since
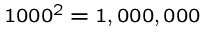 steps is reasonable
but
steps is reasonable
but 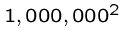 is not.
is not.
An exponential-time algorithm, i.e. 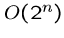 or
or 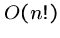 , can only be
fast enough for tiny problems, since
, can only be
fast enough for tiny problems, since 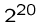 and
and 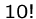 are already
up to
are already
up to 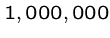 .
.
``A billion here, a billion there, and soon you are talking about
real money'' - Senator Everett Dirksen
NP-Completeness
Unfortunately, for many problems, there is no known polynomial
algorithm.
Even worse, most of these problems can be proven NP-complete,
meaning that no such algorithm can exist!
At the 1999 RECOMB conference, I witnessed a rebellion by biologists
tired of seeing all their problems shown NP-complete.
But proving a problem NP-complete can be a useful thing to do, because it
focuses our attention on heuristics and tells us why it is difficult.
NP-completeness proofs work by showing that the target problem is as
``hard'' as some famous hard problem, e.g. satisfiability, vertex cover,
Hamiltonian cycle.
Shortest Common Superstring
Input: A set
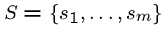 of text strings on some
alphabet
of text strings on some
alphabet 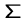 .
.
Output: The shortest possible string 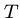 such that each
such that each 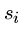 is a substring of
is a substring of 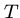 .
.
This problem arises in DNA sequence assembly.
What is the shortest common superstring of
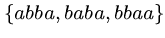 ?
?
Can you suggest an algorithm to find the shortest common superstring?
The Greedy Heuristic
The most obvious strategy is one where we merge the two strings with
the longest overlap, put the combined string back, and repeat until
only one string remains.
This greedy strategy can yield a string which is almost twice as
long as necessary:
ababababc babababab
babababab ababababc
aabababab aabababab
Optimal Greedy
The greedy heuristic for longest common superstring of 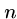 strings of
length
strings of
length 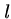 can be easily solved in
can be easily solved in 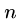 rounds of
rounds of 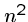 string comparisons,
each of which takes
string comparisons,
each of which takes 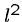 steps, for a total of
steps, for a total of 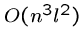 .
.
But faster implementations exist using the ``right'' data structure,
and avoiding string redundant comparisons.
Directed Hamiltonian Path is NP-Complete
The Hamiltonian cycle problem asks whether there is a tour
using the edges of a given graph such that every vertex
is visited exactly once.
When computer scientists talk about graphs, they mean networks of
nodes or vertices where certain pairs are connected by
edges.
figure=figures/hamiltonian-cycle-L.eps,width=2in
figure=figures/hamiltonian-cycle-R.eps,width=2in
The Hamiltonian path problem is well known
to be NP-complete, even if (a) every edge is directed,
(b) a particular node is designated as the start vertex, and
(c) a particular node is designated as the stop vertex.
Shortest Common Superstring is NP-Complete
We prove this by constructing an instance of SCS from any directed
Hamiltonian path problem such that any solution to the SCS gives the
Hamiltonian path.
Since Hamiltonian path cannot be solved in polynomial time, this means
that SCS also can't - because if it could then HP could!
For all edges 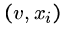 out of vertex
out of vertex 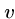 , we will construct two strings,
, we will construct two strings,
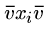 and
and
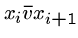 .
.
Thus if there are three edges from 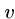 , ie.
, ie. 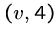 ,
, 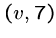 ,
, 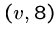 ,
we will construct the following strings:
,
we will construct the following strings:
Note that these have a superstring of length 8 starting with 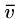 and ending with any other vertex, by breaking the cycle at the right point.
and ending with any other vertex, by breaking the cycle at the right point.
We will also construct 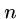 ``connector'' strings
``connector'' strings 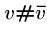 to join each vertex with its complement.
to join each vertex with its complement.
Finally, we have a start string to connect to first vertex in the path,
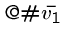 , and an end string to connect to the last vertex in the path,
, and an end string to connect to the last vertex in the path,
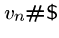 .
.
These strings have a superstring of length 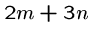 iff the graph has
a Hamiltonian path.
iff the graph has
a Hamiltonian path.
The weird characters (#, $, @) ensure there can be no shorter way
to put the strings together than the intended way.
Tools of the Trade: GenBank
GenBank is the NIH genetic sequence database, an annotated collection of all publicly available DNA sequences,
available at http://www.ncbi.nlm.nih.gov
Most journals require all relevant DNA sequences be put in GenBank before publication.
At the end of 2002, it contained
28,507,990,166 bases from
22,318,883 sequences, and it continues to almost double each year.
There is a great deal of redundancy and junk in the database - anybody can add their favorite sequence
to it.
Search programs like BLAST can check whether a sequence similar to one you are interested
in appears in GenBank.
Other interesting databases include SwissProt (a curated sequence database),
and PubMed (abstracts of the entire biomedical literature).
Example GenBank File
LOCUS AF067844 218336 bp DNA PRI 08-FEB-1999
DEFINITION Homo sapiens chromosome 10 clone PTEN, complete sequence.
ACCESSION AF067844
VERSION AF067844.1 GI:4240386
KEYWORDS HTG.
SOURCE human.
ORGANISM Homo sapiens
Eukaryota; Metazoa; Chordata; Craniata; Vertebrata; Mammalia;
Eutheria; Primates; Catarrhini; Hominidae; Homo.
REFERENCE 1 (bases 1 to 218336)
AUTHORS Jensen,K., de la Bastide,M., Parsons,R., Parnell,L.D., Dedhia,N.,
Gottesman,T., Gnoj,L., Kaplan,N., Lodhi,M., Johnson,A.F.,
Shohdy,N., Hasegawa,A., Haberman,K., Huang,E.N., Schutz,K.,
Calma,C., Granat,S., Wigler,M. and McCombie,W.R.
TITLE Genomic sequence of PTEN/MMAC1
JOURNAL Unpublished
REFERENCE 2 (bases 1 to 218336)
AUTHORS Jensen,K., de la Bastide,M., Parsons,R., Parnell,L.D., Dedhia,N.,
Gottesman,T., Gnoj,L., Kaplan,N., Lodhi,M., Johnson,A.F.,
Shohdy,N., Hasegawa,A., Haberman,K., Huang,E.N., Schutz,K.,
Calma,C., Granat,S., Wigler,M. and McCombie,W.R.
TITLE Direct Submission
JOURNAL Submitted (18-MAY-1998) Lita Annenberg Hazen Genome Sequencing
Center, Cold Spring Harbor Laboratory, 1 Bungtown Rd., Cold Spring
Harbor, NY 11724, USA
FEATURES Location/Qualifiers
source 1..218336
/organism="Homo sapiens"
/db_xref="taxon:9606"
/chromosome="10"
/clone="PTEN"
source 1..106991
/organism="Homo sapiens"
/db_xref="taxon:9606"
/chromosome="10"
/clone="BAC 265N13"
5'UTR 22308..23338
/gene="PTEN"
/note="5'-UTR defined by comparison to PTEN cDNA U93051"
mRNA join(22308..23417,51995..52079,83482..83526,89015..89058,
90987..91225,110086..110227,115821..115987,118862..119086,
123258..124345)
/gene="PTEN"
/note="mRNA coordinates delineated by comparison to PTEN
cDNA U93051"
gene 22308..124345
/gene="PTEN"
/note="the coding region of PTEN, as defined by the cDNA,
identifies 9 exons within this region; identical to MMAC1
(U92346) and PTEN (U93051)"
/evidence=experimental
exon 22308..23417
/gene="PTEN"
/function="5'-UTR and initial segment of the CDS"
/number=1
CDS join(23339..23417,51995..52079,83482..83526,89015..89058,
90987..91225,110086..110227,115821..115987,118862..119086,
123258..123443)
/gene="PTEN"
/note="coding regions delineated by comparison to PTEN
cDNA"
/codon_start=1
/product="PTEN"
/protein_id="AAD13528.1"
/db_xref="GI:4240387"
/translation="MTAIIKEIVSRNKRRYQEDGFDLDLTYIYPNIIAMGFPAERLEG
VYRNNIDDVVRFLDSKHKNHYKIYNLCAERHYDTAKFNCRVAQYPFEDHNPPQLELIK
PFCEDLDQWLSEDDNHVAAIHCKAGKGRTGVMICAYLLHRGKFLKAQEALDFYGEVRT
RDKKGVTIPSQRRYVYYYSYLLKNHLDYRPVALLFHKMMFETIPMFSGGTCNPQFVVC
QLKVKIYSSNSGPTRREDKFMYFEFPQPLPVCGDIKVEFFHKQNKMLKKDKMFHFWVN
TFFIPGPEETSEKVENGSLCDQEIDSICSIERADNDKEYLVLTLTKNDLDKANKDKAN
RYFSPNFKVKLYFTKTVEEPSNPEASSSTSVTPDVSDNEPDHYRYSDTTDSDPENEPF
DEDQHTQITKV"
exon 51995..52079
/gene="PTEN"
/number=2
source 58169..218336
/organism="Homo sapiens"
/db_xref="taxon:9606"
/chromosome="10"
/clone="BAC 60C5"
exon 83482..83526
/gene="PTEN"
/number=3
exon 89015..89058
/gene="PTEN"
/number=4
exon 90987..91225
/gene="PTEN"
/number=5
exon 110086..110227
/gene="PTEN"
/number=6
exon 115821..115987
/gene="PTEN"
/number=7
exon 118862..119086
/gene="PTEN"
/number=8
exon 123258..124345
/gene="PTEN"
/function="terminal segment of the CDS and 3'-UTR"
/number=9
3'UTR 123444..124345
/gene="PTEN"
/note="3'-UTR defined by comparison to PTEN cDNA U93051"
/evidence=experimental
BASE COUNT 64194 a 39437 c 43295 g 71406 t 4 others
ORIGIN
1 caagctttac actagagcct atatgaagtt ttgattctaa gtgttaatgt accttctgac
61 aactgtgaaa tgaaccttgt tcctggggag cgcgttctgg ttttctcttt gcacagttaa
121 gctgagacta gcatcattct agtttgcagg tgacattctc tgggaagcta gtctatgggg
181 gagatgacat cttctgaacc tagtccccac agagaacttt gaatgagtgg aatcaagagg
241 ttgcctgcat tcttgctcat gtcacaatgc tggacatgtg acttcagaga agcatgtgcc
301 aggtcaatat gattgggctg ttctcacaat acaaggcctt gaccatagag tgattcagag
361 gcaaatgcag ccttcttaga ctcttaacca aaacattggc atgacataaa attataatta
421 ataaaagata tacagttatt tcaaaagtac cgttttattg ggacatctca aaggactaag
481 aaaatgttta ttttcttatc tcctatcttt tgttaatagc tgttcatcgc tcatcagcct
541 ttactgaaag cttatcatgt atcaaacaat atgccaggtg tcagagaggg cagcaaagag
601 agtacaattg agttagatag agtacctgca ctcaataata ataacagcta acacttacat
661 agtgctttct gcgtgccagg cttgtcctaa gtgattttac acacacacac acacacacac
721 acacacacac acacacactc cctcactcag tccttataaa aacccactga taggccgggt
781 gcggtggctc atacctgtaa tcccagcaac tttgggaggc tgaagcaggc agatcacttg
841 aggtcaggag ttcgagatca ccctggccaa catggtgaaa cctcatctct actaaaaata
901 caaaaattaa ccaagcatgg tggcaggtgc ctgtaatcct agctactcaa gaggctgaga
961 caggaaaatc acttgaacct ggtaggtgga tgttgcagtg tgccgagatc gtgccaccac
1021 actccagcct gagcaacaga gtgagactct atctaaaaaa aaaaaaaaaa aaattaaaaa
217861 ggatacggtg gtgtaaaagg caaaacatat acctgatttc atggaactca cattctaggg
217921 gtggtttgtg tatatatgag aacagtaact agaaaaaaat aatgaacaag gtattttatg
217981 taacgataag agctatgaag aaaatcagac atgacgattt tcagctagag ctacccaaag
218041 catgatcttt gagtcaacaa caacatatga gcaatcagtt tgttaaaaat gcagaatctc
218101 agaagacggc ctagacctac tgattcagaa tcatcattgt aacaggatcc ccttgtcatt
218161 tctttgcatg ctaatgtttg agaagcactg agctagacag tgggaaatgg aaggtttctc
218221 tgcctaggtg acatctgagc tgagacttga atgaagaaaa gctgtccatg taaagatctg
218281 ggagcagaag gatccaggca gaggaaatgg aaagtacaag gggctggatg agagaa
//
FASTA is a simpler file format just containing the sequence data.
>gi|4240386|gb|AF067844.1|AF067844 Homo sapiens chromosome 10 clone PTEN, complete sequence
CAAGCTTTACACTAGAGCCTATATGAAGTTTTGATTCTAAGTGTTAATGTACCTTCTGACAACTGTGAAA
TGAACCTTGTTCCTGGGGAGCGCGTTCTGGTTTTCTCTTTGCACAGTTAAGCTGAGACTAGCATCATTCT
Field Definitions
Header:
LOCUS - A short mnemonic name for the entry. The line contains the Accession number, length of molecule, type of molecule (DNA or RNA), a three letter reference to possibly Taxonomy, and the date that the data was made public.
DEFINITION - A concise description of the sequence.
ACCESSION - The primary accession number is a unique, unchanging code assigned to each entry. Used often when citing sequence in journals
VERSION - The primary accession number and a numeric version number associated with the current version of the sequence data in the record. This is followed by an integer key (a "GI") assigned to the sequence by NCBI.
KEYWORDS - Short phrases describing gene products and other information about an entry.
SOURCE - Common name of the organism or the name most frequently used in the literature.
ORGANISM - Formal scientific name of the organism (first line) and taxonomic classification levels (second and subsequent lines).
REFERENCE - Citations for all articles containing data reported in this entry.
AUTHORS - Lists the authors of the citation.
TITLE - Full title of citation.
JOURNAL - Lists the journal name, volume, year, and page numbers of the citation.
MEDLINE - Provides the Medline unique identifier for a citation.
PUBMED - Provides the PubMed unique identifier for a citation.
REMARK - Specifies the relevance of a citation to an entry.
COMMENT - Cross-references to other sequence entries, comparisons to other collections, notes of changes in LOCUS names, and other remarks.
Features:
SOURCE: contains information about organism, mapping, chromosome, tissue alignment, clone identification.
CDS: instructions on how to join sequences together to make an amino acid sequence from the given coordinates. Includes cross references to other databases.
GENE Feature: a segment of DNA identified by a name.
RNA Feature: used to annotate RNA on genomic sequence (for example: mRNA, tRNA, rRNA)
Sequence:
The entire sequence.
Entrez
Entrez is a retrieval system for searching several linked databases. Databases include:
PubMed: The biomedical literature (PubMed)
Nucleotide sequence database: includes sequences from Genbank, EMBL, and DDBJ.
Protein sequence database: includes sequences from translated coding regions in the nucleotide database, and proteins submitted to PIR, SWISSPROT, PRF, and Protein DataBank (PDB)
Structure: three-dimensional macromolecular structures. MMDB (Molecular Modeling Database) contains data about crystallography and NMR specification. This data is available from PDB.
Genome: complete genome assemblies. Provides views for a variety of genomes, complete chromosomes, contiged sequence maps, and integrated genetic and physical maps.
PopSet: Population study data sets. Contains sequences that are submitted from a study describing either Evolution or Population Variation.
Taxonomy: organisms in GenBank
OMIM: Online Mendelian Inheritance in Man
Tools of the Trade: Perl
Perl is a programming language which is very widely used in
computational biology because of its power in manipulating strings of
text.
Perl stands for ``Practical Extraction and Reporting Language''.
It is especially suited for simple parsing, formating, and text
conversion problems, which arise frequently in working with web
documents and genomic sequences.
As a (typically) interpreted language, it is significantly slower
than C++, so it is not as suited for computationally-intense algorithms.
But it is designed to make simple jobs easy.
A large Perl user community exists, which has developed an extension
called bioperl which is particularly designed for working
with genomic sequences and databases.
Features of Perl
A scalar is a single number or a string:
$a = 1;
$b = "text";
Variables in Perl need not be declared before they are used.
Arithmetic operations (such as addition, multiplication etc.) work in Perl as they do in other programming languages.
Concatenation of the strings is performed with "." operator:
$b = "bb";
$c = "cc";
$a = $b . $c; # now $a is "bbcc";
An array is a list of scalars:
@bases = ("A", "C", "G", "T");
Each element of a list is a scalar. Write $bases[1] instead of bases[1] to get access to the second element of a list.
A hash is an array which elements are addressed by keywords.
The following hash represents a part of bases to acids translation table:
%translate = ("AAT", "Asn", "TAT", "Tyr", "TTT", "Phe");
To return the acid ("Asn") that the sequence "AAT" is translated to:
$translate{"AAT"};
Example: Codon to Amino Acid Translator
# convert DNA into amino acids
# read convertion table; sample line: GCG Ala
$file = "trans.dat";
open(INFO, $file);
while ($string = <INFO>)
{
$string =~ /^\s*([ACGT]{3})\s+(\w+)/ || die "Bad data: $string\n";
$trans{$1} = $2;
}
close(INFO);
# read DNA sequence
print "DNA: ";
$dna_string = <STDIN>;
# convert it to uppercase
$dna_string =~ tr/acgt/ACGT/;
# convert DNA to amino acids
print "Amino acids: ";
while ($dna_string =~ s/(^[ACGT]{3})//i)
{
print "$trans{$1} ";
}
print "\n";
Regular Expressions and String Operations
Regular expressions are perhaps the most exciting thing in Perl.
A regular expression (regexp) is a pattern representing a possibly infinite set of words. Examples:
"abc" -- single word;
"a|b" -- two words "a" and "b";
"(a|b)c" -- either ac or bc;
"ab*" -- a, ab, abb, abbb, ...
"(a|b)*" -- any string on a and b, plus the empty string.
Searching for a substring in a string can be done with "= " operator:
if ($text =~ /AAT/) { print "string has AAT"; }
Anything matched in parenthesis is remembered in variables $1,...,$9 and can be referred to later:
if ($text =~ /([A-Z]{3})/) { print "string has $1 "; }
Perl has some predefined symbols for regexps:
. # Any single character
^ # Beginning of a line
$ # End of line
\b # Word boundary
* # Zero or more matches
+ # One or more matches
[abc] # Either a, b or c
[a-zA-Z] # Any letter
\w # Any word character (the same as [a-zA-Z0-9_]
\s # Space character
String substitution can be done by using the s function:
$text =~ s/([A-Z])/:\1:/g;
This turns "TexT" into ":T:ex:T:".
The "g" option makes Perl find all occurrences of the substring; the "i" option makes Perl ignore the letter case.
BioPerl
Bioperl is a project that coordinates efforts of different developers in bioinformatics whose goal is to build a standard tools for genomic analysis. Bioperl is a set of well-documented and freely available Perl modules. Each module represents one or more objects. The core objects of Bioperl are:
Sequence - represents a single DNA sequence;
Sequence Alignment - represents a sequence alignment;
BLAST - executes commands to generate BLAST reports and analyzes them;
Alignment Factories - implements an alignment algorithm;
3D Structure - encapsulates coordinate data for 3D structures.
The Seq sequence object represents a single nucleotide sequence.
It contains methods for reading and writing sequences in different formats, including Fasta and GenBank.
The sequence object also supports other basic operations such as sequence translation, DNA to RNA conversion, and subsequence extraction.
Example BioPerl Program
This program reports sequence features within a Genbank file:
$input_seqs = Bio::SeqIO->new ('-format'=>'GenBank', '-file'=>'t7.gb');
while ( $s = $input_seqs->next_seq() )
{
print( "sequence length is ", $s->length(), "\n" );
print( "ac number is ", $s->accession(), "\n" );
foreach $f ( $s->all_SeqFeatures() )
{
print "Feature from ",$f->start," to ",$f->end," Primary tag ",
$f->primary_tag, " From", $f->source_tag(), "\n";
print "Feature description is ", $f->gff_string(), "\n";
}
}


Next: About this document ...
Up: My Home Page
Steve Skiena
2003-09-11