The primary molecules of biological interest (DNA, RNA, and proteins) all have fundamentally linear structures as a consequence of how they are replicated.
However, the biological function of these molecules depends upon how they interact with other molecules.
These interactions depend heavily upon the shape of the molecules involved.
Molecular shape/structure is determined by many factors: (1) molecular bonds, (2) electrostatic forces (i.e. positive/negative charges), (3) the size/shape of molecular subunits (amino acids and nucleotide bases), (4) hydrophobicity of the associated bases, and (5) the current environmental conditions (temperature, salinity, acidity).
Experimental methods for determining structures, such as x-ray crystalography, are slow, expensive, tricky, and work only in certain environmental conditions.
All this combines to make computational prediction of structures an important and messy problem.
The difficulties of specifying structure leads to a hierarchy of increasingly demanding notions of structure:
Primary structure usually refers to the raw sequence itself.
Secondary structure usually refers to identifying certain self-interacting features of the structure, such as which bases bond with which other bases.
Ternary structure is the complete `geometric' description of molecule; i.e. the positions of all the bases.
Quadrary structure concerns identifying how certain parts of structures interact with other structures.
The interest in these different levels of abstraction is (1) that sometimes it is much easier to get accurate predictions at lower levels, and (2) accurate lower-level knowledge may be more useful than less-precise higher-level knowledge.
DNA molecules usually come in the form of double-stranded molecules, whose secondary structure is the famous `double helix' discovered by Watson and Crick.
The ternary structure of DNA is the shape of the chromosomes it folds into.
This is a non-trivial problem - the DNA in a typical human cell would unfold to sequences 2 meters long!
When DNA is in single-stranded mode, other regulatory proteins bind at certain sites to start transcription, defining the quadrary structure.
As a single-stranded molecule, DNA folds and behaves much like RNA.
RNA molecules, like proteins, are usually single strands which fold back onto themselves into predefined 3D shapes or structures.
The folding problem seeks the structure or shape of a given sequence.
The shape of certain RNAs plays a major role in determining its interaction with other molecules, for example tRNAs.
Folding occurs in both proteins and RNA, although the issues are different.
Since RNA is single-stranded, its component bases tend to bond with other bases analogously to the bonds formed in double-stranded DNA (A-U, C-G).
The set of all these pairs constitutes the secondary structure of an RNA molecule.
In this widely used model, binding pairs partition the RNA strand into nested loops.
This model ignores pseudoknots formed when bonds are formed which do not
respect nesting constraints, i.e. ![]() and
and ![]() both form bonds even though
both form bonds even though
![]() .
.
Such pseudoknots definitely occur in nature, but are usually ignored in secondary structure prediction because (1) they make the problem too hard computationally, and (2) they might be better handled during ternary structure prediction.
A complicated energy function (derived from laboratory experiments) is used to measure the binding strength of short patterns.
Using dynamic programming Zuker, et.al has developed successful RNA secondary structure prediction algorithms - on average, 73% of known base pairs on domains of fewer than 700 nucleotides.
The simplest RNA folding model would seek the nested decomposition into bonds such that we maximize the number of bonds of complementary pairs.
We assume that the total binding energy is the sum of the energy of each of the bonds.
We can optimize by dynamic programming.
Let ![]() be the maximum number of properly-nested bonds which can be formed by the
substring from the
be the maximum number of properly-nested bonds which can be formed by the
substring from the ![]() th through
th through ![]() th bases in the sequence
th bases in the sequence ![]() .
.
Either ![]() is a bond, or they might bond with bases between
is a bond, or they might bond with bases between ![]() and
and ![]() , so:
, so:
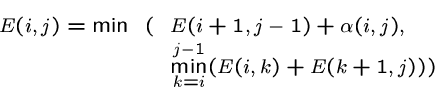
As there are ![]() cells and each can be filled in linear time, this algorithm takes
cells and each can be filled in linear time, this algorithm takes
![]() time.
time.
More general recurrences are needed to properly account for more general structures, such as (1) rewarding long runs of matched/stacked pairs, and (2) penalizing different types of loops appropriately based on size.
Let ![]() denote the minimum energy of the structure closed by
denote the minimum energy of the structure closed by
![]() .
.
The most important source of bonuses and penalties is a set of
nearest neighbor rules. An energy bonus is assigned to a
quartet of nucleotides, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , where
, where ![]() close a loop.
close a loop.
The energy of the structure closed by pair ![]() in a helix is
given by
in a helix is
given by
![]()
Penalties are assigned to hairpins according to their size, and for certain configurations of unpaired nucleotides in them.
The energy of a hairpin loop closed by ![]() is given by
is given by
![]()
The energy of an internal loop with external closing pair ![]() and
internal closing pair
and
internal closing pair ![]() is
is
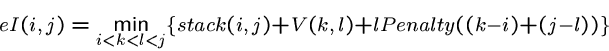
Penalties are assigned to substructures and unpaired bases within multiloops.
![]() denote the contribution of subsequence
denote the contribution of subsequence ![]() to
to ![]() ,
to a multiloop which contains
,
to a multiloop which contains ![]() to
to ![]() .
.
The energy contribution of sequence from ![]() to
to ![]() to
a multiloop is given by
to
a multiloop is given by ![]()
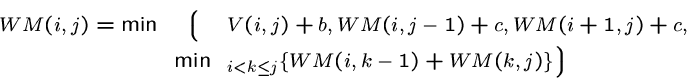
The energy of a multiloop closed by ![]() is given by
is given by
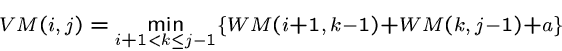
Combining these recurrences, we arrive at the composite recurrence for the minimum energy:
Because of the internal loops term, these recurrences run in ![]() .
Faster recurrences are possible, especially when there are simplifying
assumptions about the form of the penalty terms.
.
Faster recurrences are possible, especially when there are simplifying
assumptions about the form of the penalty terms.
Some RNA molecules have functions in the organism other than coding or information functions.
These functions are determined by their interaction with other molecules, which in turn is determined largely by its 3D structure.
For example, tRNA molecules transport amino acids during the process of transcription.
It is widely believed that RNA molecules are the closest thing to the molecules from which life originally evolved.
RNA molecules can perform the function of coding for proteins (information storage) usually associated with DNA.
RNA molecules can have enzymatic functions usually associated with proteins.
Thus it is easier to develop a scenario for the polymerization of nucleic acids than proteins, under the geological conditions of the young Earth.
De novo RNA structure predictions are reasonably good but not perfect.
Indeed, one problem with the dynamic programming approach (as stated) is that it returns only the single best solution, when there might be widely varying structures with almost as good energy scores.
A more accurate approach for determining the structure of functional RNAs would be to use homology information across species, since the most important structural components should be conserved in evolution.
Thus potential bonds which appear in multiple sequences are more likely to be real bonds.
Linear protein molecules rapidly fold into predefined 3D shapes or structures.
The properties of any protein is largely determined by its structure.
Proteins can be denatured by heat or chemical agents, but then fold back to their original shape.
Protein structures can be experimentally determined by crystallizing the protein and then using x-ray crystallography or NMR to find the position of the atoms, but this is a very difficult procedure.
The folded structure of a sequence is determined by the sequence of successive solid bend angles, where each solid angle can be represented by two planar angles.
Such a problem can be made discrete (at some loss of accuracy) by limiting the number of ways to bend each joint to, say, 7 solid angles.
Even so, a 100 residue protein then has a search space of ![]() configurations.
configurations.
Determining the shape of proteins from sequence is one of today's great computational challenges.
The primary structure of a protein is simply its amino acid sequence.
The secondary structure of a protein is the labeling of each
residue with whether it is part of an (1) ![]() -helix,
(2)
-helix,
(2) ![]() -sheet, or (3) a connecting loop.
-sheet, or (3) a connecting loop.
Secondary structure prediction is important because the helices and sheets determine the protein core which is typically conserved.
Different amino acids have different probabilities of appearing in each
of these structures. But beware, since there is a sequence of 5 residues
which appears in both ![]() -helix and
-helix and
![]() -sheet.
-sheet.
Although the notion of secondary structure seems somewhat
ill-defined, there are reasonably successful prediction programs
(say correctly labeling ![]() of all bases) based on ideas like
hidden Markov models.
of all bases) based on ideas like
hidden Markov models.
The 3D or tertiary structure of a protein describes the coordinates in space of each amino acid. This geometric information helps determine whether two proteins interact or dock with each other.
Protein folding programs seek to determine the tertiary structure of any protein from its sequence.
The computational difficulty of protein folding has led to proofs that the problem of finding the minimum energy configuration is NP-complete under a variety of models, e.g. maximizing the number of adjacent hydrophobic pairs in a 3D lattice model.
Leventhal's paradox is that proteins correctly fold into their pre-ordained shape less than a minute after being synthesized. How does nature solve this NP-complete problem?
Possible reasons around this problem are (1) that the theoretical models used to prove hardness are not what nature is trying to optimize, (2) evolution may have selected for proteins which fold easily, (3) proteins may well fold in locally, not globally optimal ways.
Prions, infectious agents which work by ``tricking'' proteins to fold in non-functional ways, are presumed responsible for mad-cow disease.
De novo (or ab initio) prediction programs work by defining a global energy function and does a search of possible bond-angle configurations to find one which minimizes total energy.
The process is similar watching a restless sleeper folds into the most comfortable (minimum energy) configuration.
The most important issues are (1) the energy function selected, and (2) the optimization procedure employed to search the space.
Reasonable energy minimization functions include hydrophobic/hydrophilic interactions, size and flexibility properties of different amino acids, and electrostatic / Van der Waals interactions of nearby atoms.
Standard optimization methods to employ are gradient descent, simulated annealing, genetic algorithms, and parallel computation.
IBM's Blue Gene project seeks to build a massively parallel computer for doing such de novo protein folding computations.
How can we judge how well a protein prediction program works?
One measure is to align the correct and predicted 3d structures and compute the average (RMS) deviation per residue.
Finding this alignment is not trivial, and misses the fact that the core structure is what is most important.
The CASP project/competition regularly invites structure predictions of proteins about to be experimentally determined, and determines the winner on a more ad hoc basis.
Since de novo structure prediction is hard, many programs use known 3D structures as a crutch to help folding new sequences.
This makes sense since all proteins likely descend from a small number of original structures.
Two amino acid sequences with ![]() identical residues likely have
similar three dimensional structures.
identical residues likely have
similar three dimensional structures.
Thus there may only be a small number of different folds/substructures common to all proteins, and we will likely see them all after determining a given number of structures.
In general, threading or inverse folding programs are more accurate than de novo prediction programs.
The input is (1) a protein sequence, (2) a core model describing the position of the core residues and allowable lengths of loops, and (3) a scoring function to evaluate the given threading.
Reasonable factors in the cost model include (1) the similarity of the base at each position to the original, (2) the length and similarities of the loops,and (3) pairwise interactions between bases at core positions.
Without modeling pairwise interactions, this becomes a simple dynamic programming-type problem.
However, incorporating pairwise interactions turns the problem NP-complete.
Why isn't threading just finding the best alignment with the structure model, solved with dynamic programming?
A pairwise interacting optimization function requires tabulating the possible substructures for every base assignment, not just the best matching prefix structures, so dynamic programming becomes less feasible.
Thus exhaustive search/heuristics are used in threading programs, but the options are much more constrained than for de novo folding algorithms.