1.8 Solve the recurrent relation

  (for n > 1)

We figure out the first 7 items in the sequence:

Then we know this is a cyclic sequence.

We have

  (0 <= i < 5)
 
 
 
 

1.16 Solve the recurrent relation

We guess

We always let  for the following deductions.

Let : 

We have: 

Let We have Of course here 

Let: and 

We have 

So We get 

Let 

We have 

So we get Where 

Let: g(n)=n, We get 

So: 
 
 

We get 

  Where 

2.11 Show that 

Proof:

Prove Langrange's identity

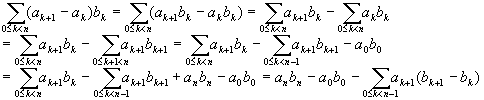
Proof:

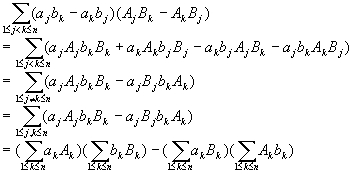
The same for the special one.
 
 
 
 

2.23a Evaluate the sum

in two ways

Hint:

8.Given a convex n-gon what is the maximum number of regions its interior can

be divided into by diagonals connecting its vertices. A triangle defineds one

region, a square with its two diagonals defines four regions, and a pentagon

with its five diagonals defines eleven regions:
 

We first give the recurrence relation:

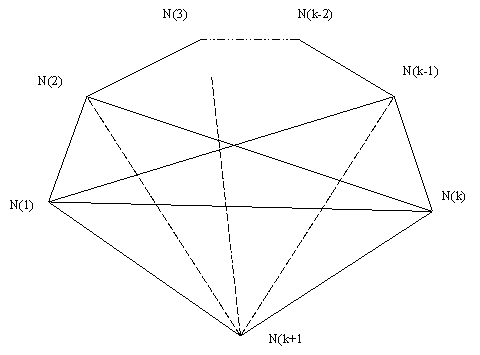
N(k+1) is the new vertex added.

Line <N(1),N(k+1)> and Line <N(k),N(k+1)> enclose a new region.
 
 

For line <N(k+1), N(i)> (2<= i <=k)

We have intersecting points on this new line, the number is:

( i - 1 ) * ( k - i )

the segments on this line should be ( i - 1 ) * ( k - i ) + 1;

every segment lead to split a region into two.

So we have the recurrence relation:

  for all n >= 3;

With initial condition R(3) = 1

We can resolve this recurrence relation.

Now give a trick.

Can be seen as selecting 3 elements from ordered n-elements set.

If the mean one selected is ith, then the first one should be chosen from

( i -1) element, and the third one in ( n - i ), So, the sum is C(n, 3)

The latter fomular has its combinatorial meaning, you can get it yourself

using the same trick i.e. selecting in n-elements ordered set.
 
 

Result: R(n)=C(n,4)+C(n-1,2)
 
 

9.Find and prove a closed form formula

Hint: k*k!=(k+1)*k! - k! = (k+1)!-k!