Exercise 7-23.
(a) Let
fn = c0, for some constant c0.
Does there necessarily exist a constant coefficient homogeneous recurrence
relation
![]() where an = bn for all n.
If so, prove it, and give d' in terms of d.
If not, give a counter-example.
where an = bn for all n.
If so, prove it, and give d' in terms of d.
If not, give a counter-example.
(b) Let
fn = c0n, for some constant c0.
Does there necessarily exist a constant coefficient homogeneous recurrence
relation
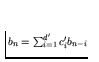 where an = bn for all n.
If so, prove it, and give d' in terms of d.
If not, give a counter-example.
where an = bn for all n.
If so, prove it, and give d' in terms of d.
If not, give a counter-example.
(c) Let
![]() ,
for some constant c0.
Does there necessarily exist a constant coefficient homogeneous recurrence
relation
,
for some constant c0.
Does there necessarily exist a constant coefficient homogeneous recurrence
relation
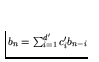 where an = bn for all n.
If so, prove it, and give d' in terms of d.
If not, give a counter-example.
where an = bn for all n.
If so, prove it, and give d' in terms of d.
If not, give a counter-example.
where A0 = A1 = 1.
where A0 = 2 and A1 = -1.