

Next: About this document ...
Up: My Home Page
Computer Science 547 - Discrete Mathematics
Prof. Steven Skiena
Spring 1999
Homework 2
Due Thursday, February 18, 1999
Each of the problems should be solved on a separate
sheet of paper to facilitate grading.
Limit the solution of each problem to one sheet of paper.
Staple all these sheets together!
Please don't wait until the last minute to look at the problems.
Do the following exercises in Graham, Knuth, and Patashnik:
- 1.
- Warmup Exercises 3.1-9. (DO NOT TURN IN)
- 2.
- Exercise 3.12.
- 3.
- Exercise 3.14.
- 4.
- Exercise 3.23.
- 5.
- Warmup Exercises 4.1-10. (DO NOT TURN IN)
- 6.
- Simplify the following sum:
It might be helpful to consult exercise 3.37 in the text.
- 7.
- Chicken McNuggets come in boxes of 6, 9, and 20, thus one can
buy them only in quantities we will call McNugget numbers:
M = 20 k1 + 9 k2 + 6 k3
Clearly, there are an infinite number of McNugget numbers.
Are there infinitely many non-McNugget numbers?
Prove or disprove the statement ``there is a largest non-McNugget number.''
- 8.
- Here is a way to test whether a number is a multiple of 7:
Take first digit, triple it, add
second digit, triple sum, and so on, finally adding last digit. If
this result is divisible by 7 so was the original number.
For example, consider 126 where
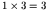 ,
,
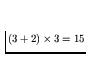 ,
15 + 6 = 21 which is divisible
by 7.
These additions and multiplications can be done mod 7.
,
15 + 6 = 21 which is divisible
by 7.
These additions and multiplications can be done mod 7.
Prove the correctness of this method.


Next: About this document ...
Up: My Home Page
Steve Skiena
1999-01-13
![]() ,
,
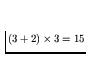 ,
15 + 6 = 21 which is divisible
by 7.
These additions and multiplications can be done mod 7.
,
15 + 6 = 21 which is divisible
by 7.
These additions and multiplications can be done mod 7.