
Next: About this document ...
Up: My Home Page
Computer Science 547 - Discrete Mathematics
Prof. Steven Skiena
Spring 1999
Homework 1
Due Tuesday, February 2, 1999
Each of the problems should be solved on a separate
sheet of paper to facilitate grading.
Limit the solution of each problem to one sheet of paper.
Staple all these sheets together!
Please don't wait until the last minute to look at the problems.
Do the following exercises in Graham, Knuth, and Patashnik:
- 1.
- Warmup exercises of chapter 1: 1-7. (DO NOT TURN IN)
- 2.
- Problem 1.8.
- 3.
- Problem 1.16.
- 4.
- Warmup exercises of chapter 2: 1-7. (DO NOT TURN IN)
- 5.
- Problem 2.11.
- 6.
- Problem 2.22.
- 7.
- Problem 2.23a.
- 8.
- Given a convex n-gon what is the maximum number of regions its interior
can be divided into by diagonals connecting its vertices.
A triangle defines one region, a square with its two diagonals defines
four regions, and a pentagon with its five diagonals defines eleven regions.
a. Formulate a recurrence for the maximum number of regions.
b. Solve that recurrence.
- 9.
- Find and prove a closed form formula for:
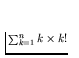


Next: About this document ...
Up: My Home Page
Steve Skiena
1999-01-13