Normal Forms
Equivalences can often be used to simplify formulas, to obtain equivalent formulas of a certain syntactic form, also called normal forms.
An advantage of normal forms is that certain questions can often be easier answered. Conjunctive and disjunctive forms are especially useful in this sense.
A propositional formula is said to be in conjunctive form if
We speak of a disjunctive form if the last condition is replaced by the condition that no disjunction occur inside any conjunction>
For example,
![]() is neither in disjunctive
nor conjunctive form,
whereas
is neither in disjunctive
nor conjunctive form,
whereas ![]() is in disjunctive form,
but not in conjunctive form.
is in disjunctive form,
but not in conjunctive form.
Construction of Normal Forms
The construction of (disjunctive or conjunctive) normal forms can be done in stages, to ensure that all three conditions will be satisfied.
For instance, we have already seen that equivalences can be used to eliminate certain connectives:
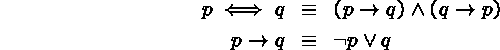
Similar equivalences can be devised to eliminate other connectives, such as exclusive-or.
Exhaustive application of these equivalences will result in a formula containing no logical connectives other than negation, conjunction and disjunction.
Negation Normal Form
A formula that satisfies the first two conditions is said to be in negation normal form.
The following additional equivalences can be employed to push negations inside of the other connectives:

Repeated application of this equivalences, from left to right, will result in a negation normal form.
Construction of Disjunctive and Conjunctive Forms
In the final stage of construction of disjunctive or conjunctive normal forms we just need to apply distributivity:
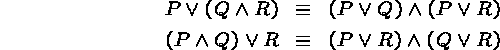
to obtain conjunctive forms, and
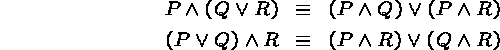
to obtain disjunctive forms.
Conjunctive forms are usually written
as ``products of sums (of literals),''
and disjunctive forms
as ``sums of products (of literals),''
where by a sum we mean a disjunction
![]() and
by a product a conjunction
and
by a product a conjunction
![]() .
A literal is either a variable p or the negation thereof,
.
A literal is either a variable p or the negation thereof, ![]() .
.
Theorem.
A formula in conjunctive form is a tautology if, and only if, each one of its sums contains both a variable and its negation.A formula in disjunctive form is a contradiction if, and only if, each one of its products contains both a variable and its negation.
Clauses
Disjunctions of literals
![]() are also called clauses.
are also called clauses.
Since a conjunction ![]() is true under a given truth assignment if,
and only if, each formula
is true under a given truth assignment if,
and only if, each formula ![]() is true,
and each propositional formula is equivalent
to a conjunctive form,
we may conclude that each propositional formula
can be represented in logically equivalent form as
a collection of clauses.
is true,
and each propositional formula is equivalent
to a conjunctive form,
we may conclude that each propositional formula
can be represented in logically equivalent form as
a collection of clauses.
For example, ![]() can be represented by the
two clauses,
can be represented by the
two clauses, ![]() and
and ![]() .
.
Each literal in a clause is either a propositional variable (a ``positive literal'') or the negation of a variable (a ``negative literal''). If a clause contains at most one positive literal, then it is called a Horn clause.
For example,
![]() and
and ![]() are Horn clauses,
but
are Horn clauses,
but ![]() is not a Horn clause.
is not a Horn clause.
An interesting aspect of Horn clauses is that they can be interpreted as program rules and used for computation, as is done in logic programming.
Logic Programming
A Horn clause ![]() is logically equivalent to the implication
is logically equivalent to the implication
![]() .
.
If the implication is known to be true,
and one wishes to prove q,
then it sufficient to show that ![]() are all true;
an observation that provides the logical basis for logic programming.
are all true;
an observation that provides the logical basis for logic programming.
A logic program is a set of Horn clauses, each containing exactly one positive literal (and zero or more negative literals). Such Horn clauses are usually written as backward implications
![]()
and called program rules.
More specifically, q is called the head of the rule,
and the sequence ![]() the body of the rule.
(Each rule must have a head, but the body may be empty.)
the body of the rule.
(Each rule must have a head, but the body may be empty.)
For example,
P(Edward VII, George V)is a logic program of six rules. The first five rules have an empty body and represent facts (about the British royal family).
P(Victoria, Edward VII)
P(Alexandra, George V)
P(George VI, Elizabeth II)
P(George V, George VI)
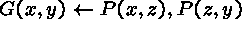
The last rule defines the grandparent relation in terms of the parent relation: a person x is a grandparent of y if there is a third person z, such that x is the parent of z, and z the parent of y.
The use of variables, such as x, y, and z, which denote individuals goes beyond the scope of propositional logic, but is crucial for the usefulness of logic programming.
Informally, the rule may be thought of as a schema representing all clauses obtained by substituting specific values for the variables, e.g.,
![]()
or
![]()
In addition to the program rules one needs to specify a goal (or a list of goals), e.g., G(Victoria, George V).
A computation with a logic program represents an attempt to derive the goal from the program rules (in an indirect way by deriving a contradiction in the form of the ``empty clause'' from the negation of the goal).
Resolution
For example, the negation of the above goal is written as a negative clause
![]()
We have also seen that suitable values may be substituted for the variables in the last program rule, so that the head is G(Victoria, George V).
This indicates that the given goal may be reduced to subgoals
![]()
Both subgoals are present as program rules and hence can be deleted, which results in the empty clause. We conclude that the original goal logically follows from the program clauses.
The logical inference rule underlying such computations is called resolution.
The propositional version of resolution for Horn clauses is:
Fromand
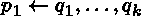
derive.
Much of the power of logic programming derives from the fact that resolution can be generalized to effectively handle clauses with variables.
For instance, if one specifies the goal
![]()
the result of the computation will be a list of all grandchildren of Victoria. A discussion of these aspects of logical programming is beyond the scope of this course.