Rumours
I've heard some disturbing rumours about this semester's CSE-113 class.
I was told that there is a student in CSE-113 such that if he or she drinks, then everybody in the class drinks!
Can that be true?
To get to the heart of this matter we must resort to some subtle reasoning methods, more powerful than those of propositional logic.
Predicate Logic
Propositional logic is very useful but often too weak in terms of its expressive power. In essence, propositional logic deals only with connections between propositions.
Predicate logic is a more general formalism with more expressive power. In particular it deals with statements of the form ``there is ...'' or ``for all ..''
Some student drinks.
All students drink.
Predicate logic analyzes connections between such sentences.
If some student drinks, then all students drink.
If all student drinks, then some student drinks.
These two sentences have the same propositional structure,
![]()
but one of them is true and the other false.
A more detailed analysis is needed.
Predicates
Propositions are sentences that can be true or false.
John takes CSE-113.
John drinks.
A predicate is a sentence with blanks, also called an open sentence or a sentence schema.
takes CSE-113.We may substitute suitable values for the blanks to obtain sentences that can be true or false.
drinks.
John takes CSE-113.
Mary takes CSE-113.
Mary drinks.
etc.
Variables
We will also look at sentence schemas with more than one blank and use variables to label blanks in a consistent way.
Variables allow us to specify more subtle subtitution schemas. Compare
drinks and takes CSE-113.with
drinks and also takes CSE-113.These are represented by two different formulas
![]()
and
![]()
When we plug in values for variables, all occurences of the same variable must receive the same value!
General predicates are of the form
![]()
where P is called a predicate symbol
and ![]() are called (predicate) variables.
are called (predicate) variables.
Domains and Truth Sets
The set of values that may be substituted for a predicate variable is called its domain.
Different variables may have different domains.
x hit more than 60 home runs in a season.
y is greater than z.
We are particularly interested the truth set of a predicate, that is, the set of those domain elements for which the predicate is true.
Truth sets define the logical meaning of a predicate.
Relations
Formally, the meaning of predicates (with one or more arguments) is given by relations.
The meaning of a predicate P that takes one argument is the set
![]()
The meaning of a predicate Q that takes two arguments is the set of pairs
![]()
The meaning of a predicate R that takes n arguments is the set of n-tuples
![]()
Predicates are syntactic expressions and relations define their semantics.
Different variables often range over different domains, in which case the above definitions need to be adjusted slightly.
Example
The two sentences
Barry Cohen is teaching section 7 of CSE-113.and
Melanie Rebosa is teaching section 10 of CSE-113.have the same structure,
is teaching section of course(but not necessarily the same truth value).
A more concise expression for this predicate is
![]()
where x denotes a person, y a section, and z a course; i.e., the three variables range over different domains.
Assigning values to variables is only one way of obtaining a (true or false) sentence from a predicate.
Quantifiers
Some student in CSE-113 drinks.These are propositions that can be true or false. They are not predicates, but in terms of logical structure are built from predicates and logical operators called quantifiers.
All students in CSE-113 drink.
In predicate logic there are two kinds of quantifiers:
Quantifers turn a predicate into a sentence:
![]()
![]()
These sentences are called universal and existential statements, respectively.
Semantics of Quantified Statements
A universal statement
![]()
is true if, and only if, F[d] is true for all domain elements d.
Thus, if just one person does not drink,
then
![]() is false.
is false.
An existential statement
![]()
is true if, and only if, F[d] is true for some domain element d.
For instance,
![]() is true:
there are two persons who teach CSE-113,
even though just one would be enough to make the statement true.
is true:
there are two persons who teach CSE-113,
even though just one would be enough to make the statement true.
Note that one often writes ![]() to indicate the domain of a quantified variable.
to indicate the domain of a quantified variable.
![]()
Examples
Some students do not satisfy the prerequisites for CSE-113.
![]()
All students who satisfy the prerequisites for CSE-113 may take the course.
![]()
Some students who drink satisfy the prerequisites.
![]()
Some students in CSE-113 drink.
![]()
If some students drink then all students drink.
![]()
![]()
The Drinking Principle
There is a student in CSE-113 such that if he or she drinks, then everybody in the class drinks.
Predicate logic formula:
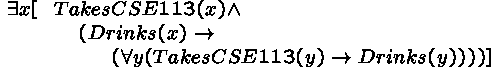
The statement is true!
To verify this we just need to find one person for which the predicate within the square brackets is true. Any student who takes CSE-113 is a candidate.
There are two cases.
(1) Suppose there is a student in CSE-113 who does not drink. Let John be such a student. Then the conjunction inside the square brackets is true, because the first conjunct is TakesCSE113(John) and the second conjunct is an implication with a hypothesis, Drinks(John), that is false.
(2) If all the students in CSE-113 drink, then we can easily check that the conjunction within the brackets is true for each one of them, because in that case the conclusion of the conditional,
![]()
is true by assumption.
In short, the statement is true.
Negations of Quantified Statements
The negation of a universal statement is logically equivalent to an existential statement:
![]()
The negation of an existential statement is logically equivalent to a universal statement:
![]()