Relations
We have seen several types of mathematical objects over the course of the semester: predicates, sets, ordered pairs, and functions.
Relations use ordered tuples to represent relationships among objects.
`` ...is a parent of ...'' - <Morris,Steve>, <Ria,Steve>
``...is a number less than ...'' - <3,42>, <42,43>
``Student number ...is named ...and majors in ...'' - <124324443,Mary,CSE>, <563565426,Mary,PSY>
``...is an even number'' ...<2>
Essentially, a relation is the set of assignments which makes a predicate true.
Binary Relations
Binary relations have two blanks, relating two objects.
More formally, suppose A and B are sets.
A binary relation from A to B is a set 
.
Thus R is a set of ordered pairs <a,b> where 
and 
.
If 
then we sometimes write a R b.
Example: 
, 
.
is ``...in A is an integer multiple of ...in B.''
so 
Presenting Binary Relations
Binary relations are particularly useful because they have two kinds of compact visual representation, tables and graphs.
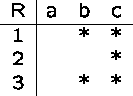
Graphs are composed of vertices or nodes connected by edges or arcs.
There is an arc from a to b iff
The Parent-Of Relation
The parent of relations, ``...is a parent of ...'', is a binary relation between pairs of people.
Which representation is better for testing whether the pair <x,y> is in the relation?
Which representation is better for capturing the overall structure?
Reflexive Relations
A relation R on A is reflexive if a is related to a (a R a)
for every .
A relation R on A is irreflexive if a is not related to
any .
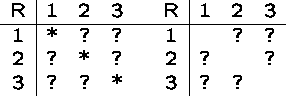
The difference is what happens on the main diagonal of the matrix.
Is the parent relation reflexive, irreflexive, or neither?
Is the 
relation reflexive, irreflexive, or neither?
Is the boss-of relation reflexive, irreflexive, or neither?
Symmetric Relations
A relation R on A is symmetric if for all 
,
whenever then 
.
A relation R on A is antisymmetric if for all ,
if and , then a=b.
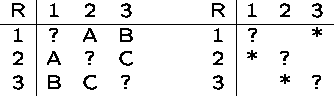
In a symmetric relation, the matrix is symmetric around the main diagonal.
In an antisymmetric relation, the only symmetric entries are one the diagonal, i.e. the only back arcs are self-loops.
Is the cousin-of relation symmetric, antisymmetric, or neither?
Is the brother-of relation symmetric, antisymmetric, or neither?
Is the relation symmetric, antisymmetric, or neither?
Transitive Relations
A relation R is transitive if for all a, b, c, if a R b and b R c, then a R c
If there is a path from a to c in a transitive relation, there must be a single arc from a to c.
Is the ancestor-of relation transitive or not?
Is the friend-of relation transitive or not?
Is the relation transitive or not?
The transitive closure of a relation R adds all the arcs to R necessary to make it transitive.
Ancestor is the transitive closure of parent.
Special and Equivalence Relations
The universal relation 
.
The empty relation 
.
The identity relation 
is an equivalence relation if it is
reflexive, symmetric, and transitive.
Equivalence relations partition the elements into equivalence classes of identically-behaving elements.
The universal and identity relations are both equivalence relations.
General (n-ary) Relations
Suppose 
, 
, ..., 
are sets.
A relation of , , ..., is a set
.
Thus R is a set of ordered n-tuples 
where 
.
Example: 
, 
, 
``Student number ...is named ...and majors in ...''
<124324443,Mary,CSE>, <563565426,Mary,PSY>
Such structures are modeled by hypergraphs, a graph structure where each ``edge'' represents a subset of more than two vertices.
Relational Databases
The most important commercial database systems today employ the relational model, meaning that the data is stored as tables of tuples, i.e. relations.
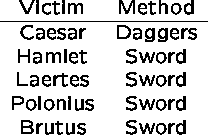
A Shakespearian killed relation would be:
Requests for information from the database is made in a query language like SQL which is based on the notations of set theory and the predicate calculus.
Example 1: Who killed Caesar?
In the relational algebra:
(KILLED WHERE VICTIM='Caesar')[KILLER]
This reads ``select from relation `killed' all tuples where the victim was Caesar, and report only the killer field from each.
Example 2: Who was both a killer and a victim?
In the relational algebra:
KILLED[KILLER] INTERSECT KILLED[VICTIM]
Much of the power of relational databases comes from the fact that we can combine different relations. For example, suppose we also have a died-by relation:
We can combine the two tables with a join operation, which the tables based on common fields. For example, the join of killed and died-by is:
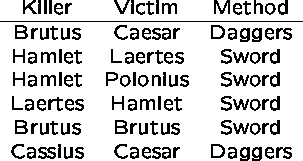
Example 3: Which killers used daggers?
In the relational algebra:
( (KILLED JOIN DIED-BY) WHERE METHOD='Daggers' ) [KILLER]
Note that this database design assumes that each victim can only be killed by one weapon (sorry, Rasputin).
Modular Arithmetic
An important example of an equivalence relation is grouping integers into classes based on their remainder mod k.
Think of grouping integers by counting around a clock.
Note that 
.
If you start at 0 and count to 23 you end up at 11.
This is because 11 and 23 have the same remainder when divided by 12.
Note that if 
and 
then 
-
think about tracing out a path on the clock to prove it.
Consider the relation 
.
This relation is reflexive, symmetric, and transitive, and hence is an equivalence relation.
What an equivalence relation means is that the elements can be partitioned into equalence classes (or blocks) such that all elements in the same block have the same properties.
, 
, ...
Total and Partial Orders
Many sets of objects, such as the integers, have a natural total order defined on them. For each pair of x and y, either (1) x > y, (2) y < x, or (3) x=y.
Such total orders can be very useful. For example, we can sort any subset of totally ordered objects uniquely, e.g. (1,5,12,14,23). The `next' element of any finite, totally ordered set is completely defined.
However, not all sets of objects have naturally defined total orders on them. Consider the set of entertainers ordered according to who is the bigger star:
Note the confusion because different types are stars are incomparable, which is not the same as equals. Several different orders are consistant with this data.
Partial Orders
is a partial order if it is reflexive,
antisymmetric, and transitive.
Examples of partial orders include ``ancestor-of'', ``less-than'', and ``divides-evenly''.
Because R is antisymmetric, there can be no cycle in R. Thus there can be no inconsistancy in the order (such as Redford-Bogart-Newman-Redford).
A partial order on n objects can have at only one consistant total ordering, or as many as n! total orderings, depending upon the pairs in the relation.
Subsets by Inclusion
For any set A, the relation 
on the power set of A defines
a partial order.
The structure of this subset inclusion relation defines the graph known as a hypercube.
Note the recursive structure of a hypercube; a d-dimensional cube is composed by connecting two (d-1)-dimensional cubes.