Finite-State Automata
In a previous lecture we discussed digital logic circuits. These were combinational circuits that implemented Boolean functions: the output values were completely determined by the input values.
In this lecture we will talk about sequential circuits, where the output depends not only on the input, but also on the prior history, or state, of the circuit.
Finite-state automata embody the essential idea of sequential circuits. They can be thought of as simple computational machines with a memory.
A Vending Machine
A vending machine dispenses pieces of candy at 20 cents each. The machine accepts only nickels and dimes and does not give change.
Its operation is shown in the following diagram.
This diagram is called a transition diagram. Each circle represents a possible ``state'' of the automaton, reflecting the amount of money that has been deposited. The arrows represent transitions from one state to another, depending on the input - ``n'' for nickel and ``d'' for dime.
Operation starts at state 0. State 20 is designated as an ``accepting state,'' in which candy is released.
Definition of an FSA
The specification of a finite-state automaton (FSA) consists of five parts:
For the vending machine example we have
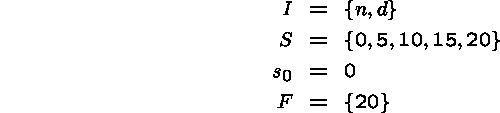
The next-state function can be represented by a table:
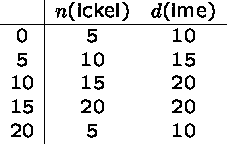
Operation of an FSA
The operation of an FSA requires a sequence of input symbols, i.e., an input string.
The computation begins at the initial state ![]() .
At each step, the machine makes a transition from
its current state s to the state s'=N(s,i),
where i is the next input symbol.
.
At each step, the machine makes a transition from
its current state s to the state s'=N(s,i),
where i is the next input symbol.
The eventual state reached by the FSA determines whether the input string is accepted or not.
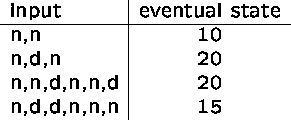
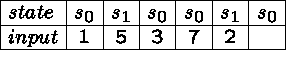
Note that the third input sequence yields two pieces of candy, whereas the last sequence yields only one piece!
We say that an input string w is accepted by an FSA A if, and only if, A goes into an accepting state when starting from its initial state and getting input sequence w.
The language accepted by A, denoted by L(A), is the set of all strings accepted by A.
Design of an FSA
We next design an FSA that accepts all bitstrings so that the number of 1's in the string is divisible by 3.
First note that if n is an integer, e.g., the number of 1's in a given bitstring, then n can be written as 3k or 3k+1 or 3k+2, for some integer k.
The following automaton keeps track of which case applies for the number of 1's that have been supplied as input symbols.
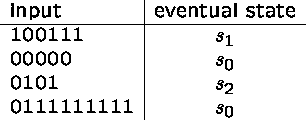
Integers Divisible by 3
Let us generalize the previous design to an FSA that takes as input a nonnegative integer in decimal representation, and determines whether it is divisible by 3.
First observe that a nonnegative integer n is divisible by 3 if the sum of its digits is divisible by 3.
We again use an automaton with three states to distinguish which of the three numbers k, k+1 and k+2, where k is the sum of all digits seen so far, is divisible by 3.
They key for the design of the FSA is in the definition of the next-state function:
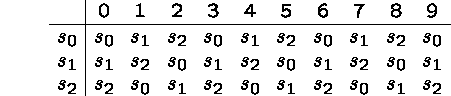
A state diagram for this automaton is shown on the next page.
FSA Accepting Integers Divisible by 3
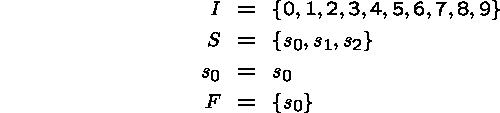
Here are sample computations:

Minimizing States in Automata
For purposes of reliability and efficiency, less is more.
Since the same problem can be solved by many different automata, we are interested in finding the machine with the fewest states which does the job.
Here are two head-counting automata which accept strings of coin tosses with an even number of heads.
The automata on the right has the smallest number of possible states.
Automata minimization algorithms work by identifying equivalence classes among the set of states, and replacing all the states in each equivalence class by one state.
These equivalence classes are built by observing that two states which have the same set of outgoing state transitions are clearly equivalent. Further, accepting states are clearly different from non-accepting states.
Building on the implications of these observations, we can refine our equivalence classes to minimize automata.
Limitations of Finite-State Automata
There are languages, i.e., sets of strings, that are not accepted by any finite-state automaton. That is, the computational mechanisms provided by finite automata may not be sufficient to express certain structural properties of strings.
An example of a language not accepted by any finite automaton
is the set L of all strings ![]() , for k a positive integer.
, for k a positive integer.
The pigeonhole principle can be used to prove that the set L is not accepted by any finite automaton. (Proof sketched in class.)