Propositional Logic
Logic deals with the formalization of natural language and reasoning methods.
A proposition is a sentence that is either true or false, but not both.
Propositional logic is the study of the structure and meaning of (simple and complex) propositions.
Key questions are:
Examples
Example simple propositions include:
Some complex propositions are:
Sentences which are not propositions include:
Propositional Formulas
In studying properties of propositions we represent them by expressions called proposition forms or formulas.
Formulas are built from propositional variables, which represent simple propositions, and symbols representing logical connectives such as and, or, not, etc.
We use the letters
p, q, r, s, ![]() to denote propositional variables
and the symbols such as
to denote propositional variables
and the symbols such as
![]() ,
, ![]() , and
, and ![]() to denote the standard logical connectives.
to denote the standard logical connectives.
Note. The term propositional logic also often refers to the formal language of propositional formulas.
Negation
We use the symbol ![]() to denote negation.
to denote negation.
Formalization (syntax): If ![]() is a formula, then
is a formula, then ![]() is also
a formula.
We say that the second formula
is the negation of the first.
is also
a formula.
We say that the second formula
is the negation of the first.
For instance,
p, ![]() , and
, and ![]() are all formulas.
are all formulas.
The similarity in the structure of a formula and its negation reflects a relationship between the meaning of propositions of this form.
Meaning (semantics): If a proposition is true, then its negation is false. If it is false, then its negation is true.
Example:
At the formula level we express the connection via a so-called truth table:
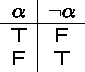
If p is true, then ![]() is false.
is false.
If p is false, the ![]() is true.
is true.
Conjunction
We use the symbol ![]() to denote conjunction.
to denote conjunction.
Syntax: If ![]() and
and ![]() are formulas, then
are formulas, then
![]() is also a formula.
is also a formula.
Semantics: If ![]() is true and
is true and ![]() is true, then
is true, then
![]() is true. In all other cases,
is true. In all other cases, ![]() is false.
is false.
Truth table:
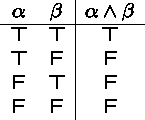
Example:
Inclusive Disjunction
We use the symbol ![]() to denote (inclusive) disjunction.
to denote (inclusive) disjunction.
Syntax: If ![]() and
and ![]() are formulas, then
are formulas, then
![]() is also a formula.
is also a formula.
Semantics: If ![]() is true or
is true or ![]() is true or both are true, then
is true or both are true, then
![]() is true. If
is true. If ![]() and
and ![]() are both false, then
are both false, then ![]() is false.
is false.
Truth table:
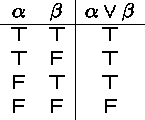
Example:
Exclusive Disjunction
We use the symbol ![]() to denote exclusive disjunction.
to denote exclusive disjunction.
Syntax: If ![]() and
and ![]() are formulas, then
are formulas, then
![]() is also a formula.
is also a formula.
Semantics:
An exclusive disjunction ![]() is true
if, and only if,
one of
is true
if, and only if,
one of ![]() or
or ![]() is true, but not both.
is true, but not both.
Truth table:
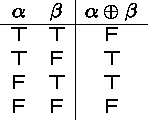
Example:
Evaluation of Formulas
The semantics of logical connectives determines how propositional formulas are evaluated depending on the truth values assigned to variables.
Each possible truth assignment or valuation for the variables of a formula yields a truth value. The different possibilities can be summarized in a truth table.
Example: ![]() (read ``p and not q'')
(read ``p and not q'')
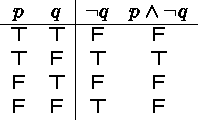
Example: ![]() (read ``p and, in addition, q or r'')
(read ``p and, in addition, q or r'')
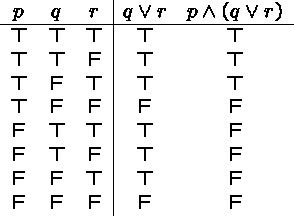
Note that it is usually necessary to evaluate all subformulas as indicated by the respective rows.
Truth Tables
A truth table for a formula lists all possible ``situations'' of truth or falsity, depending on the values assigned to the variables of the formula.
Example:
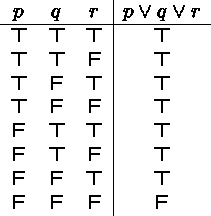
If p, q, r are the propositions ``Peter [Quincy, Richard] will lend Sam money,'' then Sam can deduce, not too surprisingly but logically correct, that he will be able to borrow money whenever one of his three friends is willing to lend him some.
Each row in the truth table corresponds to one possible situation of assigning truth values to p, q and r.
How many rows are there in a truth table with n variables? For n=1, there are two rows, for n=2, there are four rows, for n=3, there are eight rows, and so on. Do you see a pattern?
Constructing Truth Tables
There are two choices (true or false) for each of n variables, so
in general there are ![]() rows
for n variables.
rows
for n variables.
How can we construct these rows systematically?
A systematic procedure (an algorithm) is necessary to make sure you construct them all without duplicates.
The rightmost column must be computed as a function of all the truth values in the row.
Because it is clumsy and time-consuming to build large explicit truth tables, we will be interested in more efficient logical evaluation procedures.
Syntax of Formulas
The formal language of propositional logic can be specified by grammar rules.
The syntactic structure of a complex logical expression (i.e., its parse tree) must be unambiguous.

Parentheses are needed to avoid ambiguities.
For example,
the expression ![]() can be interpreted in two different ways:
can be interpreted in two different ways:
![]()
Without parentheses the meaning of the formula is not clear!
The same problem arises in arithmetic: does ![]() mean
mean
![]() or
or ![]() ?
?
Simplified Syntax
In arithmetic one often specifies a precedence among operators (say, times ahead of plus) to eliminate the need for some parentheses in certain programming languages. The same can be done for the logical connectives, though deleting parentheses may cause confusion.
The properties of the logical connectives can also be exploited to simplify the notation.
For instance, disjunction is commutative,
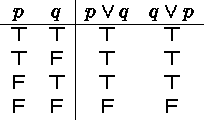
and associative,
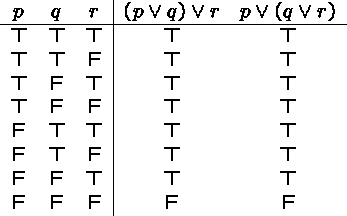
We will therefore ambiguously write ![]() to denote either
to denote either ![]() or
or ![]() .
The ambiguity is usually of no consequence,
as both formulas have the same meaning.
.
The ambiguity is usually of no consequence,
as both formulas have the same meaning.