



Next: Cuts and Tabling
Up: Tabling in Definite Programs
Previous: Tabling in Definite Programs
Contents
Index
The above description gives the general idea of how tabling affects
definite programs but is imprecise on certain points. In XSB, a
subgoal subgoals 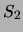 can use a table from
can use a table from 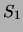 if
if 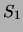 is a
variant of
is a
variant of 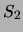 , that is, if
, that is, if 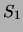 and
and 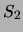 are the same up to
variable renaming. Other tabling strategies may allow
are the same up to
variable renaming. Other tabling strategies may allow 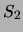 to use
the table of
to use
the table of 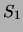 if
if 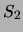 not more general than
not more general than 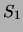 , or
, or 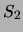 is
subsumed by
is
subsumed by 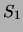 :
:
Example 5.2.1
The terms p(f(Y),X,1) and p(f(Z),U,1) are variants, but
p(f(Y),X,1) and p(f(Z),Z,1) are not. In fact, the former
subsumes the latter.
Just as a subsumption or variance relation can be used to decide when
one subgoal can use the table of another, the two relations can be
used to determine when an answer should be returned. In XSB's engine,
a derived answer 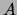 will be considered new and returned to a subgoal
will be considered new and returned to a subgoal
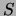 only if
only if 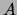 is not a variant of some other previously derived
answer for
is not a variant of some other previously derived
answer for  . In Version 2.2 of XSB, subgoal subsumption is not
supported: although work on an engine that includes subgoal subsumption
is nearing completion. Answer subsumption, however, can be flexibly
programmed as discussed in Section 5.4
5.1.
. In Version 2.2 of XSB, subgoal subsumption is not
supported: although work on an engine that includes subgoal subsumption
is nearing completion. Answer subsumption, however, can be flexibly
programmed as discussed in Section 5.4
5.1.




Next: Cuts and Tabling
Up: Tabling in Definite Programs
Previous: Tabling in Definite Programs
Contents
Index
Baoqiu Cui
2000-04-23