Project 5: Reinforcement Learning (Due: Dec 1, 2025)

Pac-Man seeks reward.
Should he eat or should he run?
When in doubt, q-learn.

Introduction

In this project, you will implement value iteration and Q-learning. You will test your agents first on Gridworld (from class), then apply them to a simulated robot controller (Crawler) and Pacman.

The code for this project contains the following files, which are available in a zip archive:

Files you will edit

Files you should read but NOT edit

Files you can ignore

What to submit: You will fill in portions of valueIterationAgents.py, qlearningAgents.py, and analysis.py during the assignment. You should submit only these files. Please don't change any others.

MDPs

To get started, run Gridworld in manual control mode, which uses the arrow keys:

python gridworld.py -m

You will see the two-exit layout from class. The blue dot is the agent. Note that when you press up, the agent only actually moves north 80% of the time. Such is the life of a Gridworld agent! 

You can control many aspects of the simulation.  A full list of options is available by running:

 python gridworld.py -h

The default agent moves randomly

 python gridworld.py -g MazeGrid

You should see the random agent bounce around the grid until it happens upon an exit.  Not the finest hour for an AI agent.

Note: The Gridworld MDP is such that you first must enter a pre-terminal state (the double boxes shown in the GUI) and then take the special 'exit' action before the episode actually ends (in the true terminal state called TERMINAL_STATE, which is not shown in the GUI).  If you run an episode manually, your total return may be less than you expected, due to the discount rate (-d to change; 0.9 by default).

Look at the console output that accompanies the graphical output (or use -t for all text). You will be told about each transition the agent experiences (to turn this off, use -q). 

As in Pac-Man, positions are represented by (x,y) Cartesian coordinates and any arrays are indexed by [x][y], with 'north' being the direction of increasing y, etc.  By default, most transitions will receive a reward of zero, though you can change this with the living reward option (-r). 

Question 1 (35 points) 

Recall the value iteration state update equation:

Value iteration computes k-step estimates of the optimal values, V_k. In addition to running value iteration, implement the following methods for ValueIterationAgent using V_k.

• computeActionFromValues(state) computes the best action according to the value function given by self.values.
• computeQValueFromValues(state, action) returns the Q-value of the (state, action) pair given by the value function given by self.values. 

These quantities are all displayed in the GUI: values are numbers in squares, q-values are numbers in square quarters, and policies are arrows out from each square.

Important: Use the "batch" version of value iteration where each vector V_k is computed from a fixed vector V_k-1 (like in lecture), not the "online" version where one single weight vector is updated in place. The difference is discussed in Sutton & Barto in the 6th paragraph of chapter 4.1.

Note: A policy synthesized from values of depth k (which reflect the next k rewards) will actually reflect the next k+1 rewards (i.e. you return π_k+1). Similarly, the q-values will also reflect one more reward than the values (i.e. you return Q_k+1). You may assume that 100 iterations is enough for convergence in the questions below.

The following command loads your ValueIterationAgent, which will compute a policy and execute it 10 times. Press a key to cycle through values, q-values, and the simulation. You should find that the value of the start state (V(start)) and the empirical resulting average reward are quite close.

python gridworld.py -a value -i 100 -k 10

Hint: On the default BookGrid, running value iteration for 5 iterations should give you this output:

python gridworld.py -a value -i 5

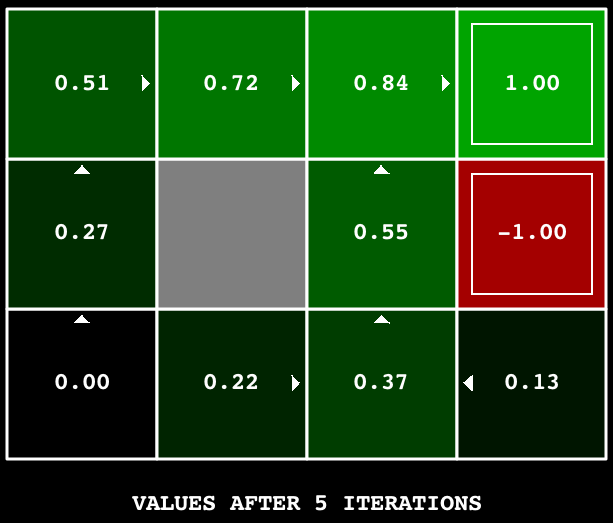
Your value iteration agent will be graded on a new grid. We will check your values, q-values, and policies after fixed numbers of iterations and at convergence (e.g. after 100 iterations).

Hint: Use the util.Counter class in util.py, which is a dictionary with a default value of zero. Methods such as totalCount should simplify your code. However, be careful with argMax: the actual argmax you want may be a key not in the counter!

Question 2 (35 points) Consider the DiscountGrid layout, shown below. This grid has two terminal states with positive payoff (shown in green), a close exit with payoff +1 and a distant exit with payoff +10. The bottom row of the grid consists of terminal states with negative payoff (shown in red); each state in this "cliff" region has payoff -10. The starting state is the yellow square. We distinguish between two types of paths: (1) paths that "risk the cliff" and travel near the bottom row of the grid; these paths are shorter but risk earning a large negative payoff, and are represented by the red arrow in the figure below. (2) paths that "avoid the cliff" and travel along the top edge of the grid. These paths are longer but are less likely to incur huge negative payoffs. These paths are represented by the green arrow in the figure below.

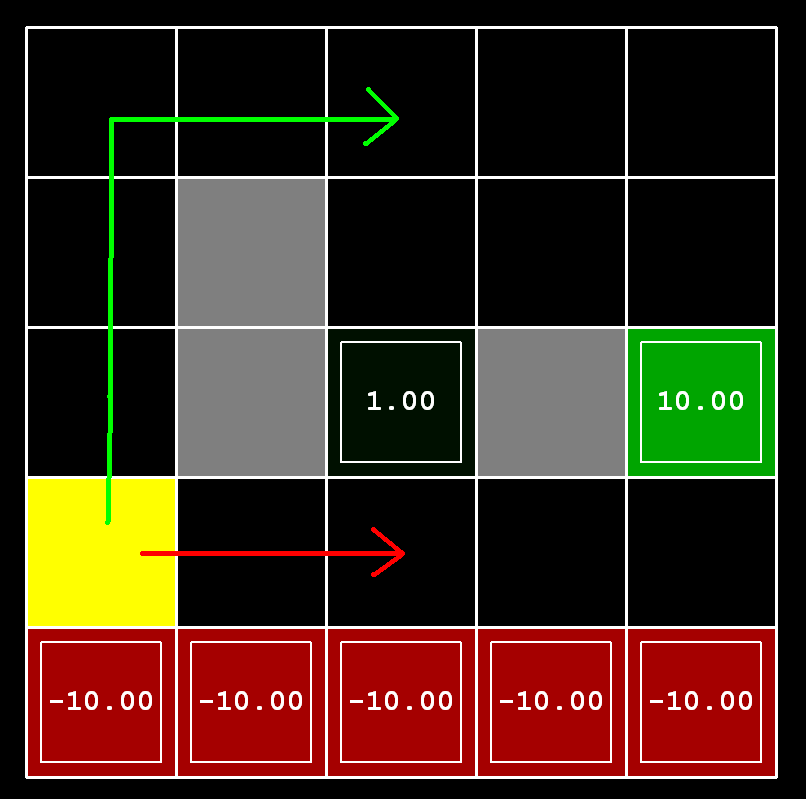
Give an assignment of parameter values for discount, noise, and livingReward which produce the following optimal policy types or state that the policy is impossible by returning the string 'NOT POSSIBLE'. The default corresponds to:

python gridworld.py -a value -i 100 -g DiscountGrid --discount 0.9 --noise 0.2 --livingReward 0.0

1. Prefer the close exit (+1), risking the cliff (-10)
2. Prefer the close exit (+1), but avoiding the cliff (-10)
3. Prefer the distant exit (+10), risking the cliff (-10)
4. Prefer the distant exit (+10), avoiding the cliff (-10)
5. Avoid both exits (also avoiding the cliff)

Note: You can check your policies in the GUI. For example, using a correct answer to 3(a), the arrow in (0,1) should point east, the arrow in (1,1) should also point east, and the arrow in (2,1) should point north.

Q-learning

Note that your value iteration agent does not actually learn from experience.  Rather, it ponders its MDP model to arrive at a complete policy before ever interacting with a real environment.  When it does interact with the environment, it simply follows the precomputed policy (e.g. it becomes a reflex agent). This distinction may be subtle in a simulated environment like a Gridword, but it's very important in the real world, where the real MDP is not available. 

Question 3 (20 points) You will now write a q-learning agent, which does very little on construction, but instead learns by trial and error from interactions with the environment through its update(state, action, nextState, reward) method.  A stub of a q-learner is specified in QLearningAgent in qlearningAgents.py, and you can select it with the option '-a q'. For this question, you must implement the update, computeValueFromQValues, getQValue, and computeActionFromQValues methods.

Note: For computeActionFromQValues, you should break ties randomly for better behavior. The random.choice() function will help. In a particular state, actions that your agent hasn't seen before still have a Q-value, specifically a Q-value of zero, and if all of the actions that your agent has seen before have a negative Q-value, an unseen action may be optimal.

Important: Make sure that you only access Q values by calling getQValue in your computeValueFromQValues and computeActionFromQValues functions.

With the q-learning update in place, you can watch your q-learner learn under manual control, using the keyboard:

python gridworld.py -a q -k 5 -m

Epsilon Greedy

Question 4 (10 points) Complete your Q-learning agent by implementing epsilon-greedy action selection in getAction, meaning it chooses random actions an epsilon fraction of the time, and follows its current best Q-values otherwise. Note that choosing a random action may result in choosing the best action - that is, you should not choose a random sub-optimal action, but rather any random legal action.

You can choose an element from a list uniformly at random by calling the random.choice function. You can simulate a binary variable with probability p of success by using util.flipCoin(p), which returns True with probability p and False with probability 1-p.

After implementing the getAction method, observe the following behavior of the agent in GridWorld (with epsilon = 0.3).

python gridworld.py -a q -k 100

Your final Q-values should resemble those of your value iteration agent, especially along well-traveled paths. However, your average returns will be lower than the Q-values predict because of the random actions and the initial learning phase.

ou can also observe the following simulations for different epsilon values. Does that behavior of the agent match what you expect?

python gridworld.py -a q -k 100 --noise 0.0 -e 0.1

python gridworld.py -a q -k 100 --noise 0.0 -e 0.9

With no additional code, you should now be able to run a Q-learning crawler robot:

python crawler.py

If this doesn’t work, you’ve probably written some code too specific to the GridWorld problem and you should make it more general to all MDPs.

This will invoke the crawling robot from class using your Q-learner. Play around with the various learning parameters to see how they affect the agent’s policies and actions. Note that the step delay is a parameter of the simulation, whereas the learning rate and epsilon are parameters of your learning algorithm, and the discount factor is a property of the environment.