The Metropolitan Transportation Authority is consulting with you regarding a new pricing scheme for New York City's subway system. In this new system, each passenger receives a ticket when they enter the subway, which indicates the station they entered at. When a passenger leaves the subway, they surrender their ticket and are charged a fee based on the distance between their origin and the current station.
The passenger is charged $1 for traveling a distance of 1 station. For every additional station, they are given a 10% discount. For example, traveling between 2 stations costs $1.90, traveling between 3 stations costs $2.70, and so on. Following this pattern, after traveling a distance of 10 stations, every additional station is free of charge.
After introducing this system, the MTA realized they were not seeing the profits they expected. Thorough investigation revealed that passengers were swapping their tickets after boarding the subway, essentially splitting the profits amongst themselves by maximizing their discounts. MTA would like you to develop a program that returns the maximum amount of profit that can be lost by this ticket swapping crisis.
We will consider only one subway and only one direction (from station 1 to station N, passing through all the stations in order) of the subway. We assume a passenger travelling from station A to B obtaining an entry card at A, can swap the entry card any number of times with any other passengers anywhere between A and B, including swapping with people who leave at A or those who enter at B, and then exit the train at B with some entry card (it is necessary to surrender some entry card to exit the subway). We also assume the passenger will not exit the train in the meantime (that is, will not surrender the currently held card and obtain a new one).
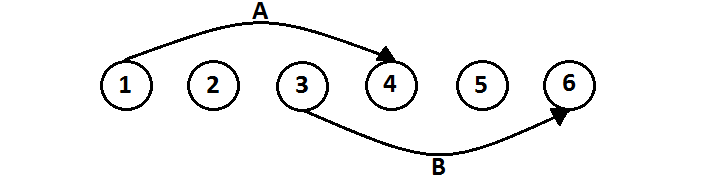
In the below example, Passenger A enters the subway at station 1 and exits at station 4, while Passenger B enters the subway at station 3 and exits at station 6.
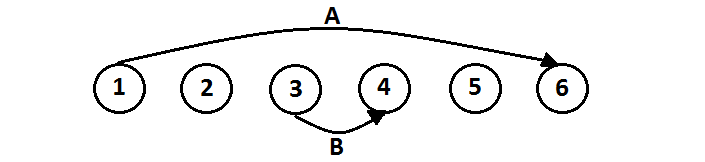
In the next example, Passenger A and Passenger B meet at station 3 and swap their tickets. It now appears Passenger A entered the subway at station 1 and
exited at station 6, while Passenger B entered the subway at station 3 and exited at station 4.
The M.T.A. associate would like you to develop a system that can determine the maximum amount of profit that can be lost by this ticket swapping crisis.
Input Format
An input file for contains the following facts:
Output format
The output should contain exactly one fact of the form loss(S), where S is the maximum amount of profit that can be lost by ticket swapping.
Example
Input |
Output |
|
passenger(paul, 1, 3). passenger(john, 3, 6). |
loss(0.6). |
|
passenger(james, 1, 3).
passenger(akshit, 1, 3). passenger(tyler, 4, 6). |
loss(0). |
|
passenger(mike, 1, 4). passenger(anna, 2, 6). passenger(susan, 4, 5). passenger(steve, 6, 7). |
loss(0.9). |
|
passenger(paul, 1, 7). passenger(john, 1, 7). passenger(peter, 6, 12). |
loss(2.5). |
| passenger(yi, 1, 3). passenger(aakash, 3, 6). passenger(richard, 1, 3). passenger(keshav, 3, 6). |
loss(1.2). |
|
passenger(alex,1,5).
passenger(bob, 2,3). passenger(chris, 3,5). passenger(dan, 5,10). |
loss(2.2). |
|
passenger(ivan, 1,3).
passenger(jin, 2,6). passenger(kyle, 3,4). passenger(lona, 4,10). |
loss(2.0). |
|
passenger(min, 1,4).
passenger(nina, 2,6). passenger(octavian, 3,4). passenger(rob, 4,10). passenger(steve, 5,20). passenger(george,3,7). |
loss(4.4). |
|
passenger(tyler, 1,3).
passenger(rob, 2,15). passenger(leo, 3,12). passenger(jennifer, 4,14). passenger(mike, 5,10). passenger(ahmad, 6,30). passenger(ritwik, 7,11). |
loss(3.1). |
Use Case 1 explained: How?
Case 1.1: If Paul pays the price from station 1 to 3, then he pays $1 + $0.9 = $1.9
John will then pay: $1 + $0.9 + $0.8 = $2.7
Total: $4.6
Case 1.2: However, if Paul swaps tickets with John, then Paul pays $0 (because he allegedly entered at station 3 and exited at station 3), while John pays $1 + $0.9 + $0.8 + $0.7 + $0.6 = $4, and MTA loses 60c.
Use Case 2: no overlaps, so no ticket swaps possible.
Use Case 3: A passenger swaps tickets more than once.
Case 3.1: Mike pays the price from station 1 to 4, $1 + $0.9 + $0.8 = $2.7
Anna pays the price from station 2 to 6, $1 + $0.9 + $0.8 + $0.7 = $3.4
Susan pays the price from station 4 to 5, $1
Steve pays the price from station 6 to 7, $1
Total = $8.1
Case 3.2: Mike swaps tickets with Anna and then swaps tickets again with Susan. It now appears that Mike entered at station 4, Anna entered at station 1, and Susan entered at station 2. Lastly, Anna swaps her ticket with Steve.
Mike's ticket (originally Susan's ticket) says he entered at station 4, so he exits at station 4 and pays $0
Susan's ticket (originally Anna's ticket) says she entered at station 2 , so she exits at station 5 and pays $1 + $0.9 + $0.8 = $2.7
Anna's ticket (originally Steve's ticket) says she entered at station 6, so she exits at station 6 and pays $0
Finally, Steve surrenders his ticket from station 1 (originally Mike's ticket) at station 7 and pays $1 + $0.9 + $0.8 + $0.7 + $0.6 + $0.5 = $4.5
Total = $7.2
Case 3.3: Mike swaps tickets with Susan, making it appear as if he entered at station 4. Next, Anna swaps tickets with Susan and then with Steve
The results and total will be exactly the same as Case 3.2, with a total of $7.2
Case 3.4: As in the previous case, Mike swaps tickets with Susan. However, this time the next move is Anna swapping tickets with Steve. Now it appears Mike entered at 4, Anna entered at 6, and Steve entered at 2. Finally, there is one more swap between Steve and Susan.
The total from Cases 3.2-3.4 are all identical, so the M.T.A. will lose a total of 90 cents.
Use Case 4: A passenger appears to travel more than 10 stations.
Case 4.1: Paul and John both pay the same price from station 1 to 7, $1 + $0.9 + $0.8 + $0.7 + $0.6 + $0.5 = $4.5 * 2 = $9
Peter pays the price from station 6 to 12, $1 + $0.9 + $0.8 + $0.7 + $0.6 + $0.5 = $4.5
Total = $13.5
Case 4.2: Paul swaps tickets with Peter, making it appear as if Paul entered at station 6 and Peter entered at station 1.
John pays the price from station 1 to 7, $1 + $0.9 + $0.8 + $0.7 + $0.6 + $0.5 = $4.5
Peter pays the price from 1 to 12 (traveling from station 11 to 12 costs him $0, since he has traveled 10 station at this point), $1 + $0.9 + $0.8 + $0.7 + $0.6 + $0.5 + $0.4 + $0.3 + $0.2 + $0.1 + $0 = $5.5
Paul pays the price from station 6 to 7, $1
Total = $11
Case 4.3: John swaps tickets with Peter, yielding the same results as Case 4.2.
The M.T.A. loses $2.5.