Brackets
(Main file name: brackets.pl)


You are preparing a lecture on parsing arithmetic expressions. Since parsing only two symbols is a good introduction to the topic, you have decided to begin the lecture by demonstrating how to parse brackets. As a part of your demonstration, you have devised a geometric representation of brackets to give your students a visual example.

The formal definition of this geometric representation is as follows: For every "(" bracket there must be a ")" bracket, making the simplest sequence "()", which represents a 1 * 1 square. If A is a correct bracket sequence and g(A) is its geometric representation, then the representation of (A) is g(A) surrounded by a rectangle that is two units wider than g(A) and one unit taller than the highest point of g(A). Furthermore, if A and B are two correct bracket sequences and g(A) and g(B) are their representations, then we get g(AB) by placing g(B) one unit to the right of g(A). The following example illustrates all of these points:



After finishing your lecture, you decide to use the geometric representations you prepared to entertain yourself. You paint the bounded areas of the images alternatively black and white, such that the outer-most areas are painted all black. After coloring the previous example, you have this as a result:



Since you love parsing expressions so much, you thoroughly enjoyed counting the numbers of black squares in these images. However, you'd like to be able to quickly check that you counted them correctly.

Input Format

An input file for LP systems contains facts of the form bracket(N,B). N (N  ≥ 0) specifies the position of the bracket in the sequence and B specifies the type of bracket, with 1 representing an open bracket "(" and -1 a closed bracket ")".

Output format

The output should consist of the fact black_squares(N), where N is the number of squares that are colored black in the geometric representation of the defined bracket sequence.

Samples


Bracket Sequence LP Input Output Geometric Representation
( ) bracket(0,1).
bracket(1,-1).
 black_squares(1).
( ( ( ) ) ) bracket(0,1).
bracket(1,1).
bracket(2,1).
bracket(3,-1).
bracket(4,-1).
bracket(5,-1).
 black_squares(10).
( ( ) ) ( ( ) ( ( ) ) ) bracket(0,1).
bracket(1,1).
bracket(2,-1).
bracket(3,-1).
bracket(4,1).
bracket(5,1).
bracket(6,-1).
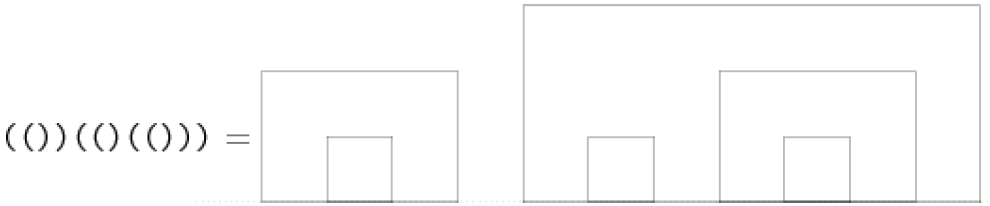
bracket(7,1).
bracket(8,1).
bracket(9,-1).
bracket(10,-1).
bracket(11,-1).
 black_squares(20).
( ( ( ) ( ( ) ) ) ) bracket(0,1).
bracket(1,1).
bracket(2,1).
bracket(3,-1).
bracket(4,1).
bracket(5,1).
bracket(6,-1).
bracket(7,-1).
bracket(8,-1).
bracket(9,-1). 		black_squares(21).
( ( ( ) ) ( ) ) ( ) bracket(0,1).
bracket(1,1).
bracket(2,1).
bracket(3,-1).
bracket(4,-1).
bracket(5,1).
bracket(6,-1).
bracket(7,-1).
bracket(8,1).
bracket(9,-1). 		black_squares(16).
( ( ( ( ) ( ) ) ) ( ) ) bracket(0,1).
bracket(1,1).
bracket(2,1).
bracket(3,1).
bracket(4,-1).
bracket(5,1).
bracket(6,-1).
bracket(7,-1).
bracket(8,-1).
bracket(9,1).
bracket(10,-1).
bracket(11,-1). 		black_squares(30).
( ) ( ( ) ) ( ( ( ) ) ) bracket(0,1).
bracket(1,-1).
bracket(2,1).
bracket(3,1).
bracket(4,-1).
bracket(5,-1).
bracket(6,1).
bracket(7,1).
bracket(8,1).
bracket(9,-1).
bracket(10,-1).
bracket(11,-1). 		black_squares(16).
( ( ( ) ) ( ( ( ) ( ) ( ) ) ) ) bracket(0,1).
bracket(1,1).
bracket(2,1).
bracket(3,-1).
bracket(4,-1).
bracket(5,1).
bracket(6,1).
bracket(7,1).
bracket(8,-1).
bracket(9,1).
bracket(10,-1).
bracket(11,1).
bracket(12,-1).
bracket(13,-1).
bracket(14,-1).
bracket(15,-1). 		black_squares(39).