Visual
Analytics and Imaging Laboratory (VAI Lab) Computer Science Department, Stony Brook University, NY |
 |
Visual
Analytics and Imaging Laboratory (VAI Lab) Computer Science Department, Stony Brook University, NY |
 |
Abstract: Oftentimes multivariate data are not available as sets of equally multivariate tuples, but only as sets of projections into subspaces spanned by subsets of these attributes. For example, one may find data with five attributes stored in six tables of two attributes each, instead of a single table of six attributes. This prohibits the visualization of these data with standard high-dimensional methods, such as parallel coordinates or MDS, and there is hence the need to reconstruct the full multivariate (joint) distribution from these marginal ones. Most of the existing methods designed for this purpose use an iterative procedure to estimate the joint distribution. With insufficient marginal distributions and domain knowledge, they lead to results whose joint errors can be large. Moreover, enforcing smoothness for regularizations in the joint space is not applicable if the attributes are not numerical but categorical. We propose a visual analytics approach that integrates both anecdotal data and human experts to iteratively narrow down a large set of plausible solutions. The solution space is first populated using a Monte Carlo procedure which uniformly samples the solution space. A level-of-detail high dimensional visualization system helps the user understand the patterns and the uncertainties. Constraints that narrow the solution space can then be added by the user interactively during the iterative exploration, and eventually a subset of solutions with narrow uncertainty intervals emerges.
Teaser: An actual use case: finding the joint distribution from a set of marginal tables with public health data (obtained from the New York Health Data query system).
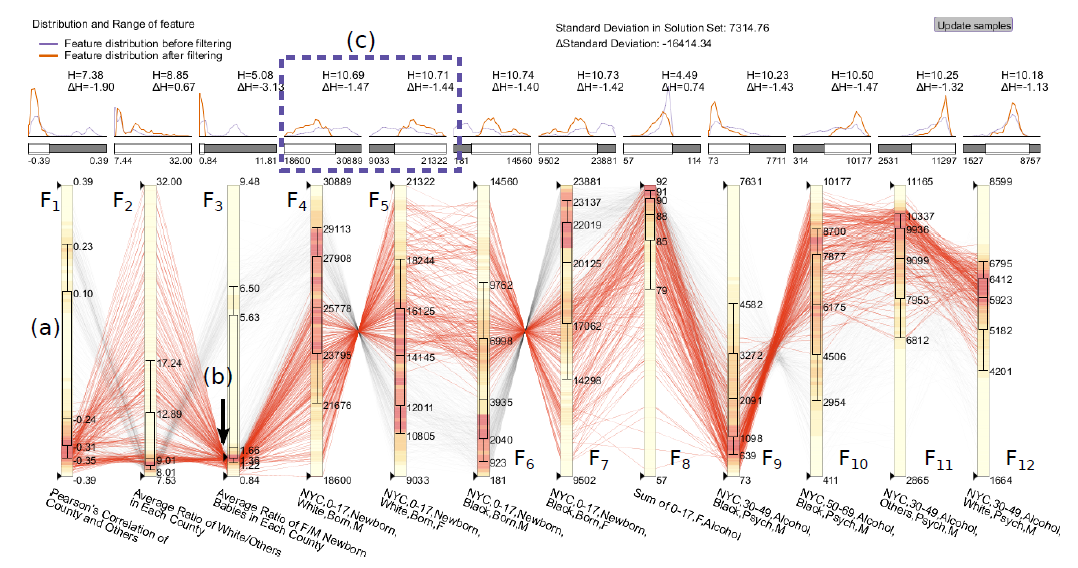
The interface of our visual analytics approach for joint distribution reconstruction. (a) Features of samples from reconstruction solution space are visualized in augmented parallel coordinates. Box plots and heat maps in axis bars show the distribution of the features. (b) The user can add constraints by filtering the range on each axis. (c) The probability density functions of the features before and after filtering are visualized in line charts. The bars below line charts show the ranges of features after filtering.
Video: Watch it to get a quick overview:
Paper: C. Xie, W. Zhong, K. Mueller, “A Visual Analytics Approach for Categorical Joint Distribution Reconstruction from Marginal Projections,” IEEE Trans. on Visualization and Computer Graphics, 23(1):51-60, 2017 (won Honorary Mention (1 of 2) Best Paper Award at IEEE VIS 2016). ppt pdf