Visual
Analytics and Imaging Laboratory (VAI Lab) Computer Science Department, Stony Brook University, NY |
 |
Visual
Analytics and Imaging Laboratory (VAI Lab) Computer Science Department, Stony Brook University, NY |
 |
Abstract: Although the Euclidean distance does well in measuring data distances within high-dimensional clusters, it does poorly when it comes to gauging inter-cluster distances. This significantly impacts the quality of global, low-dimensional space embedding procedures such as the popular multi-dimensional scaling (MDS) where one can often observe non-intuitive layouts. We were inspired by the perceptual processes evoked in the method of parallel coordinates which enables users to visually aggregate the data by the patterns the polylines exhibit across the dimension axes. We call the path of such a polyline its structure and suggest a metric that captures this structure directly in high-dimensional space. This allows us to better gauge the distances of spatially distant data constellations and so achieve data aggregations in MDS plots that are more cognizant of existing high-dimensional structure similarities. Our bi-scale framework distinguishes far-distances from near-distances. The coarser scale uses the structural similarity metric to separate data aggregates obtained by prior classification or clustering, while the finer scale employs the appropriate Euclidean distance.
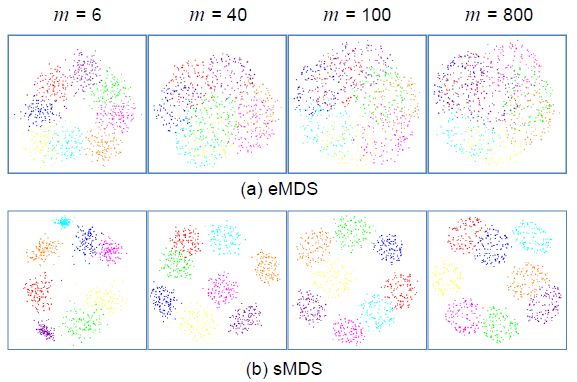
Teaser: 2D scatter plots obtained by applying MDS with (a) the Euclidean metric (eMDS) and (b) our SSIM-based metric (sMDS) to plot a synthetic Gaussian mixture dataset with 8 clusters and 800 data points (100 points for each cluster), for a variety of dimensionalities (m). A different color corresponds to a different cluster. When the number of dimensions is 6, the clusters do not overlap significantly for either metric – however eMDS shows a few overlaps. For larger numbers of dimensions, eMDS leads to severe cluster overplotting while sMDS preserves and distinguishes the individual clusters well.
Paper: J. Lee, K. McDonnell, A. Zelenyuk, D. Imre, K. Mueller, "A Structure-Based Distance Metric for High-Dimensional Space Exploration with Multi-Dimensional Scaling," IEEE Trans. on Visualization and Computer Graphics, 20(3): 351-364, 2014. pdf ppt