A Framework for the Design of Accurate and Efficient Interpolation and
Derivative Filters for Volume Rendering
In this work, we describe a new method for analyzing, classifying, and
evaluating filters, which can be applied to interpolation filters as well
as to arbitrary derivative filters of any order. Our analysis is based
on the Taylor series expansion of the convolution sum. As a result of our
analysis, we show the need and also derive the method for the normaliza
tion of derivative filter weights. Under certain minimal restrictions of
the underlying function, we are able to compute tight absolute error bounds
of the reconstruction process. As an example, we demonstrate the utilization
of our methods to the analysis of the class of cubic BC-spline filters.
As our technique is not restricted to interpolation filters, we are able
to show that the Catmull-Rom spline filter and its derivative are the most
accurate reconstruction and derivative filter, respectively, among the
class of BC-spline filters. Through our analysis of these filters we also
discover a new derivative filter which features a better spatial accuracy
than any derivative BC-spline filter, and is optimal within our framework.
Our analysis shows that a good choice of a derivative filter has a much
higher impact than the interpolation filter. We conclude by demonstrating
the use of these optimal filters for accurate interpolation and gradient
estimation in volume rendering.
For more information, see:
-
T. Moeller, R. Machiraju, K. Mueller, and R. Yagel, "Evaluation
and Design of Filters Using a Taylor Series Expansion," IEEE Transactions
on Visualization and Computer Graphics, vol. 3, no. 2, pp. 184-199,
1997.
-
T. Moeller, R. Machiraju, K. Mueller, and R. Yagel, "Classification
and local error estimation of interpolation and derivative filters for
volume rendering," Proceedings Symposium on Volume Visualization'96,
pp.
71-78, 1996.
In other work, we describe existing methods for normal estimation
in volume rendering and classify them into four classes. After showing
that three of these classes are numerically equivalent, we present a framework
to compare them with the fourth scheme. We conclude that gradient estimation
can be done in one convolution instead of two without losing numerical
accuracy. More detail is provided here:
Our latest work is motivated by the observation that for visualization
algorithms it is more natural to specify a filter in terms of the smoothness
of the resulting reconstructed function and the spatial reconstruction
error. To account for this, we present a methodology for designing filters
based on spatial smoothness and accuracy criteria. We first state our design
criteria and then provide an example of a filter design exercise. We also
use the filters so designed for volume rendering of sampled data sets and
a synthetic test function. We demonstrate that our results compare favorably
with existing methods. Here are the URLs for this work:
-
T. Moeller, R. Machiraju, Y. Kurzion, K. Mueller, and R. Yagel,
"Spatial domain filter design," (in review) 1998.
-
T. Moeller, K. Mueller, Y. Kurzion, R. Machiraju, and R. Yagel,
"Design
of accurate and smooth filters for function and derivative reconstruction",Proceedings
Symposium on Volume Visualization'98, pp. 143-151, 1998.
This research effort is still on-going, and the M^3 Y^2 team, Torsten
Moeller, Raghu Machiraju, Klaus Mueller, Roni Yagel and Yair Kurzion, works
relentlessly and restlessly to improve the quality of your datasets.
SOME IMAGES:
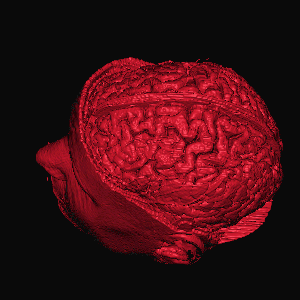
View onto an MRI brain dataset
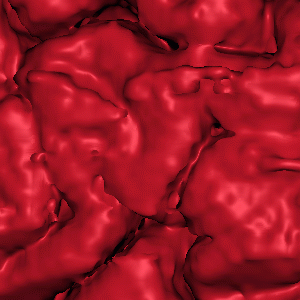
Zoomed in at high magnification:
 |
 |
discontinuous filter, 1EF
(grid is very noticable)
|
discontinuous filter, 3EF
(grid is less noticable)
|
 |
 |
C0 continuous filter, 1EF
(smooth)
|
C0 continuous, 3EF
(smooth, but more detail)
|
Thus, it is important to use a filter that is both smooth and has a
high order of error function (EF).
To
Research Homepage





