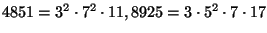- (a)
- There are real numbers a and b such that
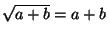 .
.
One such example is a=0 and b=0, therefore the statement is true
- (b)
- There is a real number x so that
2x > x10
x=0 is such a number since 20=1 and 010=0.
- (c)
- Definition: an integer n is called a perfect square
iff n=k2 for some integer k. Prove there is a perfect
square that can be written as a sum of two other perfect
squares.
from the pythagorean theorem 32 + 42 = 52.
- (d)
- The sum of any two odd integers is an even integer
write the odd integers as n=2j+1 and m=2k+1. Then their sum is n+m = 2j+1+2k+1 = 2(j+k+1) which is obviously divisible by two.
- (e)
- For all positive integers n, if n is prime then n is
odd.
This is not true, because 2 is a prime number and a positive integer
Theorem: The product of an even integer and an odd integer is even.
proof: ``Suppose m is an even integer and n is an odd integer. Ifis even, then by definition of even there exists an integer r such that
. Also, since m is even, there exists an integer p such that m = 2p and since n is odd there exists an integer q such that n=2q+1. Thus
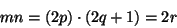
where r is an integer. By definition of even, then, mn is even, as was to be shown.''
the mistake is that the proof begs the question: it starts out by supposing that mn is even, which is exactly what you're supposed to be proving.
- (a)
- Is 52 divisible by 13?
yes:
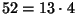 .
.
- (b)
- Is 51 divisible by 17?
yes:
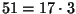 .
.
- (c)
- Is
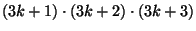 divisible by 3?
divisible by 3?
yes:
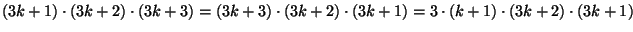 which is
clearly divisible by 3.
which is
clearly divisible by 3.
- (d)
- Is
2m (2m + 2) divisible by 4?
yes: 2m (2m + 2) = 4m(m+1) = 4(m2 +m) which is divisible by 4.
- (e)
- Is
6a (a + b) a multiple of 3a?
yes:
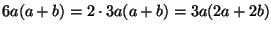 which
is a multiple of 3a.
which
is a multiple of 3a.
- (f)
- If a is divisible by b and a is divisible by c then
a is divisible by bc
no: if a=10, b=5, c=5 then a is divisible by b and a is divisible by c but a is not divisible by bc
- (g)
- If a is divisible by b and a is divisible by c then
a is divisible by b+c
no: if a=15, b=3, c=5 then a is divisible by b and a is divisible by c but a is not divisible by b+c
- (h)
- If a is divisible by b and a is divisible by c then
a is divisible by b-c
no: if a=10, b=5, c=2 then a is divisible by b and a is divisible by c but a is not divisible by b-c
- (i)
- If a is divisible by b and a is divisible by c then
a is divisible by b+c
no: if a=10, b=5, c=2 then a is divisible by b and a is divisible by c but a is not divisible by b+c
- (j)
- if
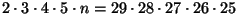 ,
then is n divisible by 29? Why?
,
then is n divisible by 29? Why?
yes: 29 is a prime number. Yet
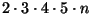 is divisible by 29 since it's equal to
is divisible by 29 since it's equal to
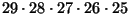 ,
since 29 is a prime number you can't
multiply two integers together to get it, which means that 29 must be
a factor of n which is the same thing as saying n is divisible byu
29. Another (simpler) way is like this:
,
since 29 is a prime number you can't
multiply two integers together to get it, which means that 29 must be
a factor of n which is the same thing as saying n is divisible byu
29. Another (simpler) way is like this:
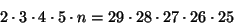
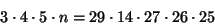
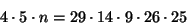
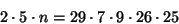
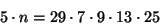
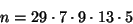
which clearly shows n is divisble by 29. - (k)
- Use the unique factorization theorem to write 4851 and 8925 in
standard factored form.