CSE 305 Final Examination

Wednesday, December 17, 2003, 5-7:30 pm (150 minutes)

Total Points: 100

• Open books and open class notes. No other printed material allowed.

• Violations of honor code will be dealt with strictly.

• We recommend that you do the rough work separately (back of the papers) and write only your answers neatly in the space provided.

1. (0 points) Identity. Please print your name and student ID.
   1. Name: _______________________________.
   2. ID: _______________________________.































2. (10 points) E/R Diagrams. Consider the following ER diagram showing students and courses. The diagram represents two relationships 'isTaking' and 'TAfor' with obvious meanings. Change the diagram so that a student cannot TA a course that he is taking. You may change the diagram in any way you wish (removing/adding attributes, entities, relationships, etc.).
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
3. (5 points) Functional Dependencies. Is the following statement true? If so, prove it. Otherwise, disprove it. Note: You just need a counterexample (i.e., a table R(A,B,C) with tuples) to disprove a statement.
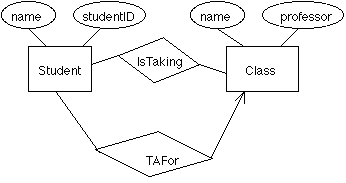
   • If AB->C, then A->B or A->C.

   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

4. (10 points) Functional Dependencies. Consider a relation R(A,B,C). Suppose R contains the following four tuples: {(1,2,3), (1,2,4), (5,2,3), (5,2,6)}. List all nontrivial multivalued dependencies that hold on R. Note that there are only 6 possible nontrivial MVDs in R.
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
5. (10 points) Relational Algebra. Consider the relation StockPrice(symbol, date, price), which stores the daily closing price of each stock for each trading day. Find all the stocks that rose more than MSFT on 12/12/2003, i.e., find all stocks B such that the following holds:

   ((price of B on 12/12/2003) - (price of B on 12/11/2003)) is greater than 
   ((price of MSFT on 12/12/2003) - (price of MSFT on 12/11/2003)).
   

   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
6. (15 points) SQL Queries Consider the following relational schema:
   • StockPrice (symbol, date, price)
   • StockHolding (SSN, symbol, numberOfShares)
     

   Each person holds a certain number of shares of each company. This information is stored in the StockHolding relation. You may assume that the holdings of a person are permanent (never changed/changes). Write the following queries in SQL.

   1. For each person, find the total portfolio value on 12/12/2003. Total portfolio value of a person on 12/12/2003 is defined as the sum of "((number of shares held) times (stock price on 12/12/2003))" over all symbols held in one's portfolio.
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   2. Find all people who had a total portfolio value of greater than $1 million on 12/12/2003, but whose ortfolio value on 6/12/2003 was half of their portfolio value on 12/12/2003.
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
7. (20 points) Sparse/Dense Indexes. Consider a sequential file (sorted by attribute A) consisting of 1,000,000 records. Each block can either store 10 records or 50 key-pointer pairs or 200 pointers.
   
   
   1. How large (in blocks) would a first-level sparse index (on attribute A) be on the file?
      
      
      
      
      
      
      
      
      
      
   2. We now construct a second-level index on the index of part (a). How large (in blocks) would the second-level index be?
      
      
      
      
      
      
      
      
      
      
      
      
   3. Next, we construct a separate secondary index on another attribute B. The index uses indirection as shown in Figure 13.17 of the textbook. For each B attribute value found in the file, there are at most 3 records that share that B-value. Compute the minimum size (in blocks) of the index.
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
8. (10 points) Size Estimation. Consider three relations R(A,B), S(B,C), and T(C,D) each having 100,000 tuples. Assume V(R,A) = 50, V(R,B) = 100, V(S, B) = 100, V(S,C) = 200, V(T,C) = 100, and V(T,D) = 300. What is the estimated size of ((R NATURAL-JOIN S) NATURAL-JOIN T)? Assume that V(R NATURAL-JOIN S, C) = V(S,C).
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
9. (20 points) Query Optimization. Consider the join of two relations R and S. Each relation has 10,000 tuples that are stored contiguously on disk, occupying 1000 blocks each. The join will be performed using 201 blocks of available memory.
   1. What is the minimum amount of memory needed to perform a merge-sort join (including the _full_ sorting operation)?
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
   2. What is the cost of the join operation in (a) ?
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
   3. Now, consider the hash-join operation with the amount of memory we have. What is the minimum number of buckets that can be produced? How large is each bucket?